Let original length = 100 and original breadth = 100
Then original area = 100 × 100 = 10000
Length of the rectangle is halved
=> New length = $\dfrac{\text{Original length}}{2}=\dfrac{100}{2}=50$
Breadth is tripled
=> New breadth= Original breadth × 3 = 100 × 3 = 300
New area = 50 × 300 = 15000
Increase in area = New Area - Original Area = 15000 - 10000= 5000
Percentage of Increase in area = $\dfrac{\text{Increase in Area}}{\text{Original Area}} \times 100$
$=\dfrac{5000}{10000} \times 100=50\% $

O is the centre of the circle and the mid-point of BC.DO is parallel to AC.
So, $\angle$DOB=$60^{o}$
Area of $\triangle$BDO=$\dfrac{49\sqrt{3}}{4}$
Area of sector OBD=$\dfrac{49\pi}{6}$
Hence area of the shaded region
=$2\left(\dfrac{49\pi}{6}-\dfrac{49\sqrt3}{4}\right)cm^{2}$
=$49\left(\dfrac{\pi}{3}-\dfrac{\sqrt3}{2}\right)cm^{2}$
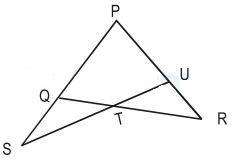
We have QT=TR and PU=PS.UR=2 units
We draw RV $\parallel$ PS that meets SU extended at V.
In $\triangle$QST and $ \triangle$TVR
$\angle$QTS=$\angle$VTR [Opposite angles]
$\angle$QST=$\angle$TVR [Alternate angles as PS$\parallel$VR]
QT+TR
$\therefore\triangle$QST and $\triangle$TVR are congruent.
$\therefore$QS=VR -------- (i)Now
$\angle$QST=$\angle$PUS=$\angle$VUR=$\angle$UVR
$\therefore$ In $\triangle$UVR
$\angle$VUR=$\angle$RVU
or,
RV=UR=2 -------- (ii)
From (i) and (ii)
QS=VR=UR=2units
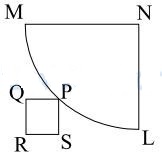
It is given that RS passes through L and RQ passes through M.
On drawing the line RSL and RQM, the diagram shown above results. From the diagram, it is clear that MNLR has to be a square and P has to be the mid point of the arc.
As P is the mid-point of the arc, RN passes through P,
As NP is radius, it length is a.
Now,
RP=RN-NP, where RN is diagonal of the square with length $=\sqrt{a^2+a^2}=a\sqrt{2}$ and NP=a
Putting values,
RP=RN-NP
RP=$a\sqrt{2}-a$
RP=$a(\sqrt{2}-1)$
RP=$a\left(\sqrt{2}-1\right)$
where MN=PN=a
PQ=$\dfrac{RP}{\sqrt{2}}$
$a\sqrt{2}-a / \sqrt{2}$
$MN^{2}:PQ^{2}=2:3-2\sqrt{2}$
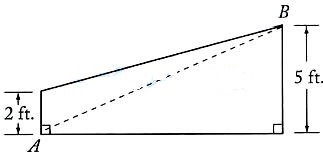
The formula for calculating the area of a trapezoid is
$Area=\dfrac{1}{2}\left(base1+base2\right)\left(height\right)$
The bases of the trapezoid are given as 2 feet and 5 feet, so only the height (AQ) needs to be found.
Since the dashed line AB=13 feet, and triangle BQA is a right triangle, use the Pythagorean theorem to calculate AQ.Thus,
AQ=$\sqrt{13^{2}-5^{2}}$
=$\sqrt{144}$
=12
Substituting the values into the formula for calculatingthe area of a trapezoid:
$Area=\dfrac{1}{2}\left(2+5\right)\left(12\right)$
=42 square feet

Vertical angles are congruent, so $150^{o}+150^{o}=300^{o}$ of the circle is not shaded.
Since there are $360^{o} $in a circle, this makes
$360^{o}−300^{o}=60^{o}$ of the circle shaded.
The fraction of the circular region that is shaded is thus
=$\dfrac{60}{360}$
=$\dfrac{1}{6}$
Let the width of the road be x meters.
Then, (60 – 2x)(40 – 2x) = 2109
=> 2400 – 200x + 4$x^{2}$ = 2109
=> 4$x^{2}$ – 200x + 291 = 0
=> x = (200 ± 188) / 8 = 1.5 or 48.5
But width of road cannot be greater than breadth of the park. Thus, width of road = 1.5m.

The lawn is in the form of a rectangle with two semicircles on opposite ends of the width.
Area of the rectangle = 200m x 14m = 2800 sq. m
Radius of the semicircles = $\dfrac{14}{2}$ m = 7 m
Area of the two semicircles = $2\times\left(\dfrac{\pi R^{2}}{2}\right)$
=$ \dfrac{22}{7} \times 7 \times 7 $
= 154 sq. m.
Area of circle = $\pi R^{2}$
=100 sq. cm
$R^{2}=\dfrac{100}{\pi}$ Or, $R =\dfrac{10}{\sqrt{\pi}}cm$
From the figure, side of square, a = Radius of circle, $R = \dfrac{10}{\sqrt{\pi}}cm$
Diagonal of the square = $a{\sqrt{2}}$
$=\dfrac{10}{\sqrt{\pi}}\sqrt{2}cm$

Let's first divide the diagram of the house into two rectangles and a trapezoid, since we can calculate the area of each of these figures.
Now, the area of the larger rectangle=$40 feet \times 20 feet$
$=800 feet^{2}$
The area of the smaller rectangle=$25 feet \times 6 feet$
=$150 feet^{2}$
The area of the trapezoid A=$\dfrac{1}{2}h\left(b1+b2\right)$
The height (h) is 6 feet, and the two bases (b1 and b2) are 8 and 11 feet.
A=$\dfrac{1}{2}6\left(8+11\right)$
A=$\dfrac{1}{2}6\left(19\right)$
=$57feet^{2}$
Therefore Adding all three areas gives a total area of the house =800+150+57
$= 1,007 feet^{2}$
