பொது அறிவியல் விதிகள்
ஆற்றல் அழிவின்மை விதி- ஆற்றலை, ஆக்கவோ, அழிக்கவோ முடியாது.
- ஒருவகை ஆற்றலை மற்றொரு வகை ஆற்றலாக மாற்ற முடியும்.
- எந்த ஓர் ஆற்றல் மாற்றத்திலும் மொத்த ஆற்றலின் அளவு மாறாமல் இருக்கும்.
பாஸ்கல் விதி
- நீர்மங்களின் அடிப்பகுதியில் அழுத்தம், அந்நீர்மத்தின் மொத்த உயரத்தைப் பொருத்தது.
- நீர்மங்கள் அவை உள்ள கலனின் பக்கங்களிலும் அழுத்தத்தை கொடுக்கின்றன.
- திரவங்கள் ஒரே ஆழத்தில், ஒரே அளவு அழுத்தத்தைக் கொடுக்கின்றன.
- திரவங்களில் ஆழம் அதிகரிக்க அழுத்தம் அதிகரிக்கும்.
- திரவங்களின் அழுத்தம் அவற்றின் அடர்த்தியைப் பொருத்தது.
எதிரொளிப்பு விதி
- படுகதிர், எதிரொளிப்புக் கதிர், படுபுள்ளியில் வரையப்பட்ட குத்துக்கோடு ஆகியவை ஒரே தளத்தில் அமையும்.
- படுகோணமானது எதிரொளிப்புக் கோணத்திற்குச் சமம்.
- $\lfloor I$ = $\lfloor r$
- I - படுகோணம்
- r - எதிரொளிப்புக் கோணம்
ஆர்க்கிமிடிஸ் தத்துவம்
- ஒரு பொருள், பாய்மத்தில் (திரவம் (அ) வாயு) தங்கு தடையின்றி முழ்கியிருக்கும் போது, அது இழப்பதாகத் தோன்றும் எடை, வெளியேற்றப்படும் பாய்மத்தின் எடைக்குச் சமமாக இருக்கும்.
மிதவை விதிகள்
- மிதக்கும் பொருளின் எடையானது, அதனால் வெளியேற்றப்படும் திரவத்தின் எடைக்குச் சமம்.
- மிதக்கும் பொருளின், ஈர்ப்பு மையமும் வெளியேற்றப்படும் திரவத்தின் ஈர்ப்பு மையமும் (மிதவை மையம்) ஒரே செங்குத்துக்கோட்டில் அமைய வேண்டும்.
பாயில் விதி
- வெப்பநிலை மாறாமல் உள்ள போது குறிப்பிட்ட நிறையுள்ள வாயுவின் அழுத்தம் அதன் கன அளவிற்கு எதிர்த்தகவில் அமையும்.
- $P\propto\dfrac{1}{v}$
- Pv - மாறிலி; P - அழுத்தம் ; v - கன அளவு
சார்லஸ் விதி
- அழுத்தம் மாறாமல் உள்ள போது வெப்பநிலை மற்றும் கன அளவிற்கான தொடர்பைத் தருகிறது.
இருவிதிகள்
- கன அளவு விதி
- அழுத்த விதி
கன அளவு விதி
- அழுத்தம் மாறாமல் உள்ளபோது குறிப்பிட்ட நிறையுள்ள வாயுவின் கன அளவு (v) அதன் கெல்வின் வெப்பநிலைக்கு (T) நேர்த்தகவில் அமையும்.
$V\propto T $
- $\dfrac{V}{T}$= மாறிலி
அழுத்த விதி
- கன அளவு மாறாமல் உள்ள போது குறிப்பிட்ட நிறையுள்ள வாயுவின் அழுத்தம் அதன் கெல்வின் வெப்பநிலைக்கு நேர்த்தகவில் அமையும்.
$P\propto T $;
- $\dfrac{P}{T}$= மாறிலி
டாப்ளர் விளைவு
- ஒலி மூலத்திற்கும், கேட்குநருக்கும் இடையில் ஒரு சார்பியக்கம் உள்ள போது,ஒலியின் அதிர்வெண்ணில் தோற்ற மாற்றம் ஏற்படும் நிகழ்வு டாப்ளர் விளைவு.
நியூட்டன் முதல் விதி / இயக்கத்திற்கான முதல் விதி
- சமமற்ற புறவிசையொன்று செயல்பட்டு மாற்றும் வரை எந்த ஒரு பொருளும் தனது ஓய்வு நிலையையோ அல்லது நேர்க்கோட்டில் அமைந்த சீரான இயக்க நிலையையோ மாற்றிக் கொள்ளாமல் தொடர்ந்து அதே நிலையில் இருக்கும்.
நியூட்டனின் இரண்டாம் இயக்க விதி
- பொருளின் மாறுபாட்டு வீதம், அதன் மீது செயல்படும் விசைக்கு நேர்த்தகவில் அமைவதோடு அவ்விசையின் திசையிலேயே அமையும்.
- $F\propto ma$;
- F=ma
- F - விசை ; m - நிறை ; a - முடுக்கம்
நியூட்டனின் மூன்றாம் இயக்க விதி
- ஒவ்வொரு வினைக்கும் அதற்குச் சமமான ஆனால் எதிர் திசையில் செயல்படும் ஓர் எதிர்வினை உண்டு.
நியூட்டனின் ஈர்ப்பு விதி
- அண்டத்திலுள்ள ஒவ்வொரு பொருளும், மற்ற பொருள்களை, அவற்றின் நிறைகளின் பெருக்கற்பலனுக்கு $(m1\times m2)$ நேர்த்தகவிலும், இடைத்தொலைவின் இருமடிக்கு $(r^{2})$ எதிர்த்தகவிலும் அமைந்த விசையுடன் ஈர்க்கும்.
- F=$\dfrac{Gm1m2}{d^{2}}$
- G - மாறிலி ;
- m1, m2 - நிறைகள் ; d- பொருள்களுக்கிடையேயான தொலைவு
ஓம் விதி
- மாறா வெப்பநிலையில் கடத்தி ஒன்றின் வழியே பாயும் மாறா மின்னோட்டம் அதன் முனைகளுக்கு இடையேயுள்ள மின்னழுத்த வேறுபாட்டிற்கு நேர்த்கவில் இருக்கும்.
- $V\propto I$
- $\dfrac{V}{I}$=மாறிலி
- V= IR
- R - மின்தடை
- V - மின்னழுத்தம்
- I - மின்னோட்டம்
ஜூல் வெப்ப விதி
ஒரு மின்தடையில் உருவாக்கப்படும் வெப்பமானது, குறிப்பிட்ட மின்தடைக்கு அதன் வழியே பாயும்.
- மின்னோட்டத்தின் இருமடிக்கு $(I^{2})$ நேர்விகிதத்திலும்
- குறிப்பிட்ட மின்னோட்டத்திற்கு மின்தடையாக்கியின் மின்தடைக்கு (R)நேர்விகிதத்திலும்.
- மின்தடையாக்கியின் வழியே மின்னோட்டம் பாயும் நேரத்திற்கு நேர்விகிதத்திலும் (t) இருக்கும்
- H = $I^{2} Rt$
H - வெப்பநிலை
I - மின்னோட்டம்
R - மின்தடை
t - நேரம் (விநாடி)
பிளமிங் இடக்கை விதி
இடக்கையின் கட்டைவிரல், சுட்டு விரல், நடுவிரல் ஆகிய மூன்றையும் ஒன்றுக்கொன்று செங்குத்தாக வைக்கவும்.
- சுட்டுவிரல் காந்தப் புலத்தின் திசையையும்
- நடுவிரல் மின்னோட்டத்தின் திசையையும் குறித்தால் கட்டைவிரல் கடத்தி இயங்கும் திசையை குறிக்கும்

பிளமிங் வலக்கை விதி
வலக்கையின் சுட்டுவிரல், நடுவிரல், பெருவிரல் மூன்றையும் ஒன்றுக்கொன்று நேர்க்குத்தாக வைக்கவும் .
- சுட்டுவிரல் காந்தப்புலத்தின் திசையையும்
- பெருவிரல் கடத்தி இயங்கும் திசையையும் குறித்தால்
- நடுவிரல் தூண்டு மின்னோட்டத்தின் திசையைக் குறிக்கும்.
ஒளிவிலகல் விதி
- படுகதிர், விலகுகதிர், படுபுள்ளியில் அவ்விரு ஊடகங்கள் சந்திக்கும் பரப்பிற்கு வரையப்பட்ட செங்குத்துக்கோடு ஆகியவை ஒரே தளத்தில் அமையும்.
- ஒளியானது ஓர் ஊடகத்திலிருந்து மற்றோர் ஊடகத்திற்கு செல்லும்.
ஸ்நெல் விதி
ஒளியின் குறிப்பிட்ட வண்ணத்தையும் குறிப்பிட்ட ஊடகங்களையும் பொருத்தவரை படுகோணத்தின் சைனுக்கும் (Sin i) விலகுகோணத்தின் சைனுக்கும் (Sin r) உள்ளதகவு மாறிலி
$\dfrac{Sin\:i}{Sin\:r}$=மாறிலி
i - படுகோணம் ; r - விலகுகோணம்
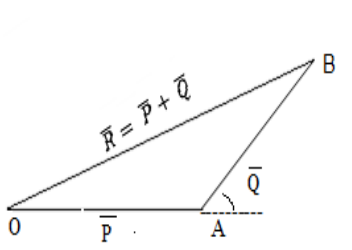
வெக்டர்களின் முக்கோண விதி
எண் மதிப்பிலும், திசையிலும் குறிக்கப்பட்ட இரு வெக்டர்கள் வரிசைப்படி ஒரு முக்கோணத்தில் அடுத்தடுத்தப் பக்கங்களாகக் கருதப்பட்டால், அவற்றின் தொகுப்பயன், எதிர்வரிசையில் அந்த முக்கோணத்தின் மூடிய பக்கமாக இருக்கும்.
நேர்க்கோட்டு உந்த அழிவின்மை விதி
- அமைப்பு ஒன்றின் மொத்த உந்தம் எப்போதுமே மாறாது.
- புறவிசைகளின் தாக்கம் கழி எனில், அமைப்பின் மொத்த உந்தம் மாறாமல் இருக்கும்
ஹீக் விதி
- ஒரு கம்பியின் நீட்சிக்கும், அதில் ஏற்படும் மீள்விசைக்கும் இடையே உள்ள தொடர்பை விளக்கும்.
- மீட்சி எல்லைக்குள் ஒரு பொருளின் திரிபானது அதை ஏற்படுத்தக் கூடிய தகைவுக்கு நேர்தகவில் உள்ளது.
தகைவு $\propto$ திரிபு
தகைவு/திரிபு= மாறிலி
இது மீட்சிக் குணம் எனப்படும்.
ஸ்டோக் விதி
- அதிக பாகுநிலை கொண்ட நீர்மத்தினூடே கீழ்நோக்கி நகரும் ஒரு பொருள் அதனுடன் தொடர்பு கொண்ட ஏடுகளை இழுக்கும். இதனால் ஏடுகளுக்கிடையே ஒப்புமை இயக்கும் ஏற்படுகிறது.
- இந்த ஒப்புமை இயக்கம் காரணமாக கீழ்நோக்கிய பொருளின் மீது பாகுநிலை (F) விசை செயல்படுகிறது.
F=$6\pi\eta a V$
n – பாகியல் எண்
a - கோள பொருளின் ஆரம்
V - கோள வடிவ பொருளின் திசைவேகம்
ஆற்றல் சமபங்கீட்டு விதி
வெப்பம் சமநிலையில் இயங்கும் தொகுதியின் மொத்த ஆற்றல் தொகுதியின் அனைத்து உரிமைப்படிகளுக்கும் சமமாகப் பங்கிடப்படுகிறது.இது ஆற்றல் சம பங்கீட்டு விதியாகும்.
வெப்ப இயக்கவியலின் சுழி விதி
- தொகுதிகள் A, B, C யைக் கருத்தில் கொள்வோம்.
- இரு தொகுதிகள் (A, B) என்பன, தனித்தனியே மூன்றாவது தொகுதியுடன் (C) வெப்பச் சமநிலையில் இருந்தால், அம்மூன்று தொகுதிகளும் ஒன்றோடொன்று வெப்பச் சமநிலையில் இருக்கும்.
வெப்ப இயக்கவியலின் முதல் விதி
ஓர் அமைப்பிற்கு கொடுக்கப்ட்ட வெப்ப ஆற்றல், அமைப்பின் அக ஆற்றல் மாறுபாடு, மற்றும் அமைப்பினால் செய்யப்பட்ட வேலை, இவற்றின் கூடுதலுக்கு சமம்.
$\triangle Q$=$\triangle W + \triangle U$
$\triangle Q$ - கொடுக்கப்பட்ட வெப்ப ஆற்றல்
$\triangle W$ - செய்யப்பட்ட வேலை
$\triangle U$ - அக ஆற்றல்
வெப்ப இயக்கவியலின் இரண்டாம் விதி
இவ்விதி, ஆற்றல் மாறுபாட்டின் அளவு மற்றும் திசையைப் பற்றிக் கூறுகிறது.
கெல்வின் கூற்று
- ஒரு பொருளை, அதன் சூழலை விட, மிகக் குளிர்ந்த வெப்பநிலையைக் காட்டிலும், குறைவாக உள்ள வெப்பநிலைக்கு குளிர்விப்பதன் மூலம் அதனின்றும் தொடர்ந்து வேலையைப் பெற முடியாது.
கிளாசியஸின் கூற்று
- புற உதவியின்றி தானே இயங்கும் இயந்திரத்தின் மூலம் குறைந்த வெப்பநிலையில் உள்ள ஒரு பொருளிலிருந்து அதிக வெப்பநிலையிலுள்ள மற்றொரு பொருளுக்கு வெப்பத்தை மாற்ற இயலாது.
கெல்வின் பிளாங்க் கூற்று
- வெப்பத்தினை, வெப்ப மூலத்திலிருந்து பெற்று, அதற்குச் சமமான வேலையைச் செய்யும் ஒரு சுற்றில் இயங்கும் வெப்ப இயந்திரத்தினை அமைக்க இயலாது.
கிர்ச்சாஃப் விதி
- ஒரு குறிப்பிட்ட அலைநீளத்தின் மற்றும் வெப்பநிலையில் கதிர்வீச்சு திறனுக்கும் உட்கவர் திறனுக்கும் உள்ள தகவு மாறிலி.
$\dfrac{e_\lambda}{ a_\lambda}$ = மாறிலி
$e_\lambda$ - கதிர்வீச்சு திறன்
$a_\lambda$ - உட்கவர் திறன்
வியனின் இடப்பெயர்ச்சி விதி
- பொருளின் வெப்பநிலை (T) அதிகரிக்கும் போது, பெரும் ஆற்றலுக்குரிய அலைநீளமானது $(\lambda_{m})$ குறைகிறது
$\lambda_{m}\propto\dfrac{l}{T}$
$\lambda_{m} T=b$
b - வியன்மாறிலி
b = $2.898 x 10^{-3} mk$
ஸ்டீஃபனின் விதி
- முழுக் கரும்பொருள் ஒன்றின் ஓரலகுப் பரப்பினின்றும் ஒரு நொடியில் வெளிவிடப்படும் மொத்த வெப்ப ஆற்றல் (E) அதன் கெல்வின் வெப்பநிலையின் நானமடிக்கு $(T^{4})$ நேர்த்தகவில் உள்ளது
- $E\propto T^{4}$
- $E=\sigma T^{4}$
- $\sigma $ ஸ்டீஃபன் மாறிலி ;$\sigma $= $5.67 X 10^{-8}wm^{2}k^{-4}$
- இது ஸ்டீஃபன் போல்டஸ்மன் விதி எனவும் அழைக்கப்படுகிறது.
நியூட்டனின் குளிர்வு விதி
- உயர் வெப்பநிலையிலள்ள ஒரு பொருள் வெப்பத்தை இழக்கும் வீதம்,அப்பொருளுக்கும், சுற்றுப்புறச் சூழலுக்கும் இடையிலான வெப்பநிலை வேறுபாட்டிற்கு நேர்த்தகவில் இருக்கும்.
டேஞ்ஜென்ட் விதி
- ஒன்றுக்கொன்று நேர்க்குத்தான இரு காந்தப் புலங்கள் செயல்படும் புள்ளியில் தொங்கவிடப்பட்டுள்ள காந்த ஊசியானது, அவ்விரு புலங்களின் தொகுபயன் புலத்தின் திசையில் ஓய்வு நிலைக்கு வரும்.
கூலும் விதி
- இரு புள்ளி மின்னூட்டங்களுக்கு இடையேயான கவர்ச்சி விசை அல்லது விரட்டு விசையானது (F) மின்னூட்டங்களின் பெருக்குத் தொகைக்கு நேர்த்தகவிலும் (q1, (2) அவற்றிற்கு இடையே உள்ள தொலைவின் இருமடிக்கு $(r^{2})$ எதிர்த்தகவிலும் அமையும்.
- மின்னூட்டங்களை இணைக்கும் கோட்டின் வழியே விசையின் திசை அமையும்.
- $F \propto \dfrac{q_{1}q_{2}}{r^{2}}$
- F =$K\dfrac{q_{1}q_{2}}{r^{2}}$
K-விகித மாறிலி;
K=$\dfrac{1}{4\pi \epsilon_{0}}$
K=$9 \times 10^{9} Nm^{2} C^{-2}$
காஸ் விதி
- எந்தவொரு மூடிய பரப்பில் செயல்படும் மின்புலத்தின் மொத்த பாய மதிப்பு, அப்பரப்பில் உள்ள மொத்த மின்னூட்டத்தின் $\dfrac{1}{\epsilon_{0}}$ மடங்கிற்குச் சமம்.
$\phi$=$\dfrac{q}{\epsilon_{0}}$
$\phi$ - மின்புல பாயம்.
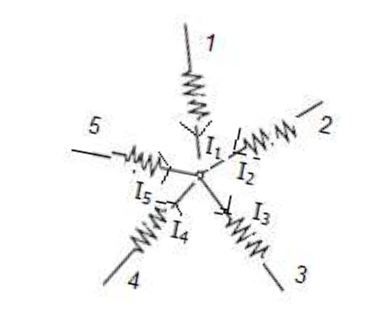
கிர்ச்சாஃபின் முதல் விதி (மின்னோட்ட விதி)
- ஒரு மின்சுற்றில், எந்தவொரு சந்திப்பிலும், சந்திக்கின்ற மின்னோட்டங்களின் குறியியல் கூட்டுத்தொகை சுழியாகும்.
- சந்தியை நோக்கிச் செல்லும் மின்னோட்டங்கள் $I_{1},I_{4},I_{5}$ நேர்க்குறி உடையன.
- சந்தியில் இருந்து வெளிச் செல்லும் மின்னோட்டங்கள் $I_{2},I_{3}$, எதிர்க்குறி உடையன.
- $I_{1}+(-{I_{2}})+(-{I_{3}})+I_{4}+I_{5}$=0
- $I_{1},I_{4},I_{5}$=$I_{2},I_{3}$
- இவ்விதி மின்னூட்ட அழிவின்மை விதியின் படி செயல்படுகிறது.
கிர்ச்சாஃபின் இரண்டாம் விதி
- ஒரு மூடிய மின்சுற்றின் வெவ்வேறு பகுதிகளில் உள்ள மின்தடை (R) மற்றும் மின்னோட்டம் (I) ஆகியவற்றைப் பெருக்கிவரும் அளவுகளின் குறியியல் கூட்டுத்தொகை அம்மூடிய சுற்றில் உள்ள மின்னியக்கு விசைகளின் குறியியல் கூட்டுத் தொகைக்குச் சமம்.
- ABCD என்ற மூடியப் பாதையைக் கருதினால்
- மின்னோட்டம் $I_{1},I_{4},I$
- மின்த டை $R_{1},R_{2},R_{3},R_{4}$
- மின்னியக்கு விசை $E_{1},E_{2}$
- அகமின்தடை $r_{1},r_{2}$
- $I_{1}R_{2}+I_{2}R_{3}+I_{2}r_{2}+I_{3}R_{4}+I_{1}R_{1}$=$E_{1}E{2}$
- இவ்விதி ஆற்றல் அழிவின்மை விதியின் படி செயல்படுகிறது.

ஃபாரடேயின் மின்னாற்பகுதல் விதிகள்
முதல் விதி
- மின்னாற் பகுத்தலின் போது மின்வாயில் வெளிப்படும் பொருளின் நிறையானது மின்பகு திரவத்தின் வழியே பாயும் மின்னூட்டத்திற்கு நேர்த்தகவில் அமையும்.
$m\propto q$
m - நிறை ;q - மின்னூட்டம்
q = IT;
I - மின்னோட்டம் ;t - நேரம்
$m\propto It$m=zIt
z - மாறிலி ; மின்வேதிய எண்
ஃபாரடேயின் இரண்டாம் விதி
- மின்பகு திரவத்தின் வழியே குறிப்பிட்ட அளவு மின்னூட்டம் செலுத்தப்படும் போது,ஒரு மின்வாயில் வெளிப்படும் தனிமத்தின் நிறை, அத்தனிமத்தின் வேதிய இணைமாற்றுக்கு நேர்த்தகவில் இருக்கும்.
- $m\propto E$
m - நிறை ;E - வேதிய இணை மாற்று
மேக்ஸ்வெல்லின் வலக்கை திருகு விதி
- மின்னோட்டம் பாயும் கடத்தியைச் சுற்றி அமைந்துள்ள காந்தவிசைக் கோடுகளின் திசையானது, வலது கை திருகு ஒன்றினை மின்னோட்டம் செல்லும் திசையில் செலுத்தும் போது, திருகு சுழலும் திசையால் பெறப்படும்.
பயட்-சாவர்ட் விதி
மின்னோட்டம் பாயும் கடத்தியைச் சுற்றி ஏற்படும் காந்தப்புலம் சார்ந்துள்ள காரணிகள் பற்றி விளக்குகிறது.
காந்தத் தூண்டல்- மின்னோட்டத்திற்கு (I) நேர்த்தகவிலும்
- மின்னோட்டக் கூறின் நீளத்திற்கு நேர்விகிதத்திலும் (dl)
- கோண சைன் மதிப்பிற்கு $sin \theta$ நேர்த்தகவிலும்
- தொலைவின் இருமடிக்கு ($r^{2}$) எதிர்த்தகவிலும் இருக்கும்.
- $dB\propto \dfrac{Idl sin \theta}{r^{2}}$
ஆம்பியரின் சுற்று விதி
- எந்தவொரு மூடிய வளைக்கோட்டிலும் சுற்றிய காந்தப் புலத்தின் கோட்டு வழித் தொகையீட்டு மதிப்பு ${\oint}\overline{B}.\overline{dl}$ ஆனது. உட்புகுத்திறன் $\mu_{0}$ மற்றும் வளைகோட்டால் மூடப்பட்ட பரப்பு வழியே பாயும் மின்னோட்டம் ஆகியவற்றின் பெருக்கற்பலனுக்குச் சமம்.
- ${\oint}\overline{B}.\overline{dl}$= $\mu_{0}I_{0}$
- $\mu_{0}$ - உட்புகுத்திறன்
- $I_{0}$ - மூடப்பட்ட பரப்பு வழியே பாயும் மின்னோட்டம்
முனை விதி
- ஒரு முனையிலிருந்து நோக்கும் போது வரிச்சுருள் வழியே பாயும் மின்னோட்டம் வலஞ்சுழியாக அமைந்தால் அருகே உள்ள முனை தென்முனை ,சேய்மையில் உள்ள முனை வடமுனை.
மின்காந்தத் தூண்டல் பற்றிய ஃபாரடே விதிகள்
முதல் விதி
- ஒரு மூடப்பட்ட கற்றோடு தொடர்பு கொண்ட காந்தப் பாயம் மாறும் பொழுது அந்த கற்றில் மின்னியக்கு விசை தூண்டப்படுகிறது. காந்தப் பாயத்தின் மாற்றம் நிகழ்ந்து கொண்டிருக்கும் வரையில் மட்டுமே தூண்டப்பட்ட மின்னியக்கு விசை நீடிக்கும்.
- மூடப்பட்ட கற்றில் தூண்டப்பட்ட மின்னியக்கு விசையின் எண்மதிப்பு, சுற்றுடன் தொடர்பு கொண்ட காந்தப் பாயம் மாறும் வீதத்திற்கு நேர்த்தகவில் இருக்கும்.
$e\propto\dfrac{\phi_{2}-\phi_{1}}{1}e\propto\dfrac{d\phi}{dt}$
லென்ஸ் விதி
- ஒரு சுற்றில் தூண்டப்பட்ட மின்னோட்டத்தின் திசை, எப்போதும் அதை உருவாக்கக் காரணமாக இருந்த, காந்தப் பாய மாற்றத்தை எதிர்க்கும் வகையில் அமையும்.
புருஸ்டர் விதி
- தளவிளைவுக் கோணத்திற்கும், ஒளி விலகல் எண்ணிற்கும் இடையேயான தொடர்பு பற்றி விளக்குகிறது.
- தள விளைவுக் கோணத்தில் ஒளிக்கற்றை படும் போது எதிரொளிக்கும் கதிரும், விலகலடைந்த கதிரும் ஒன்றுக்கொன்று செங்குத்தாக அமையும்.
- $\dfrac{sin\:i_{p}}{sin\:i_{r}}$=$\mu$
- தளவிளைவுக் கோணத்தின் டேஞ்சன்ட் மதிப்பு எண்ணளவில் அந்த ஊடகத்தின் ஒளிவிலகல் எண்ணிற்குச் சமம்.
- $tan\:i_{p}$=$\mu$
மோஸ்லே விதி
- சிறப்பு $\times$ கதிர் நிறமாலையில் தோன்றும் நிறமாலை வரியின் அதிர்வெண் $(\lambda)$ உமிழும் தனிமத்தின் அணு எண்ணின் (z) இருமடிக்கு நேர்விகிதத்தில் இருக்கும்.
- $\lambda \times z^{2}$
- $\sqrt{\lambda}$ = a(z - b)
a, b – நிறமாலை வரிக்கான மாறிலி
ஒளியின் உமிழ்தலின் விதிகள்
விதி : 1
- குறிப்பிட்ட ஒளி உணர்திறன் மிக்க பொருளிற்கு, ஒளியின் செறிவு எவ்வளவு அதிகம் இருப்பினும், எந்த அதிர்வெண்ணிற்கும் கீழ் ஒளியின் உமிழ்தல் முற்றிலும் நிகழாதோ, அந்த படுகதிரின் சிறும அதிர்வெண் பயன் தொடக்க அதிர்வெண் எனப்படும்.
விதி : 2
- குறிப்பிட்ட ஒளி உணர்திறன் மிக்க பொருளிற்கு, படுகதிர்வீச்சின் அதிர்வெண் ஆனது பயன் தொடக்க அதிர்வெண்ணை விட அதிகமாக இருக்கும்போது, ஒளி மின்னோட்டமானது படுகதிரின் செறிவிற்கு நேர்த்தகவில் இருக்கும்.
விதி : 3
- ஒளிமின் உமிழ்வு ஒரு உடனடி நிகழ்வாகும். அதாவது கதிர்வீச்சு படுவதற்கும், ஒளி எலக்ட்ரான்கள் உமிழப்படுவதற்கும் இடையில் காலப் பின்னடைவு இருக்காது.
விதி : 4
- ஒளி எலக்ட்ரான்களின் பெரும் இயக்க ஆற்றல் படுகதிரின் அதிர்வெண்ணிற்கு நேர்த்தகவில் இருக்கும்: செறிவினைச் சார்ந்தது அல்ல.
கதிரியக்கச் சிதைவு விதி
- ஓரலகு நேரத்தில் சிதைவடையும் அணுக்களின் எண்ணிக்கை (சிதைவு வீதம்) அந்நேரத்தில் அத்தனிமத்தில் உள்ள அணுக்களின் எண்ணிக்கைக்கு நேர்தகவில் அமையும்.
