Through T, the mid-point of the side QR of a $\triangle$ PQR , a straight line is drawn to meet PQ produced to S and PR at U, so that PU=PS. If length of UR=2 units then the length of QS is
$2\sqrt{2}units$
$\sqrt{2} units$
2 units
5 units
Explanation:
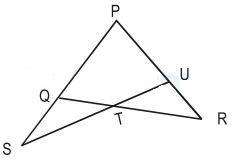
We have QT=TR and PU=PS.UR=2 units
We draw RV $\parallel$ PS that meets SU extended at V.
In $\triangle$QST and $ \triangle$TVR
$\angle$QTS=$\angle$VTR [Opposite angles]
$\angle$QST=$\angle$TVR [Alternate angles as PS$\parallel$VR]
QT+TR
$\therefore\triangle$QST and $\triangle$TVR are congruent.
$\therefore$QS=VR -------- (i)Now
$\angle$QST=$\angle$PUS=$\angle$VUR=$\angle$UVR
$\therefore$ In $\triangle$UVR
$\angle$VUR=$\angle$RVU
or,
RV=UR=2 -------- (ii)
From (i) and (ii)
QS=VR=UR=2units
