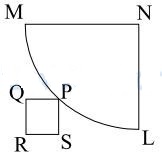
In the figure given below MN and NL are adjacent sides of a square and the arc MPL is drawn with N as centre and MN as radius. P is a point on the arc and PQRS is a square such that, RS, if extended, passes through L while RQ, if extended, passes through M. What is the ratio of the area of a square of side MN and the square PQRS?
It is given that RS passes through L and RQ passes through M.
On drawing the line RSL and RQM, the diagram shown above results. From the diagram, it is clear that MNLR has to be a square and P has to be the mid point of the arc.
As P is the mid-point of the arc, RN passes through P,
As NP is radius, it length is a.
Now,
RP=RN-NP, where RN is diagonal of the square with length $=\sqrt{a^2+a^2}=a\sqrt{2}$ and NP=a
Putting values,
RP=RN-NP
RP=$a\sqrt{2}-a$
RP=$a(\sqrt{2}-1)$
RP=$a\left(\sqrt{2}-1\right)$
where MN=PN=a
PQ=$\dfrac{RP}{\sqrt{2}}$
$a\sqrt{2}-a / \sqrt{2}$
$MN^{2}:PQ^{2}=2:3-2\sqrt{2}$