In Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that

For Competitive Exams

Question 3 In Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that $\dfrac{ar (ABC)}{ar (DBC)} = \dfrac {AO}{DO}$

Solution:

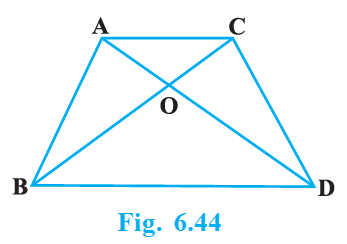
Given,

ABC and DBC are two triangles on the same base BC. AD intersects BC at O

We have to prove:

$\dfrac{Area (ΔABC)}{Area (ΔDBC)}$ = $\dfrac{AO}{DO}$

Let us draw two perpendiculars AP and DM on line BC

We know that area of a triangle = $\dfrac{1}{2}$ × Base × Height

$\dfrac{ar (\triangle ABC)}{ar(\triangle DEF)} = \dfrac{\frac{1}{2}\times BC \times AP}{\frac{1}{2}\times BC \times DM} = \dfrac{AP}{DM}$

In ΔAPO and ΔDMO

$\angle APO = \angle DMO$ (Each 90°)

$\angle AOP = \angle DOM$ (Vertically opposite angles)

∴ ΔAPO ~ ΔDMO (AA similarity criterion)

∴$\dfrac{AP}{DM} = \dfrac{AO}{DO}$

$\dfrac{Area (ΔABC)}{Area (ΔDBC)} = \dfrac{AO}{DO}$

Additional Questions

If the areas of two similar triangles are equal, prove that they are congruent.	Answer
D, E and F are respectively the mid-points of sides AB, BC and CA of Δ ABC. Find the ratio of the areas of Δ DEF and Δ ABC.	Answer
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.	Answer
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.	Answer
Tick the correct answer and justify : ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is	Answer
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio	Answer
Let Δ ABC ~ Δ DEF and their areas be, respectively, $64 cm^2$ and $121 cm^2$. If EF = 15.4 cm, find BC.	Answer
Diagonals of a trapezium ABCD with AB \|\| DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.	Answer
In Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that $\dfrac{ar (ABC)}{ar (DBC)} = \dfrac {AO}{DO}$		Answer
If the areas of two similar triangles are equal, prove that they are congruent.	Answer

Share with Friends