Given, ΔABC ~ ΔDEF
Area of ΔABC = 64 $cm^2$
Area of ΔDEF = 121 $cm^2$
EF = 15.4 cm
$\dfrac{Area \: of \: angle \: \triangle ABC}{Area \: of \: angle \: \triangle DEF} = \dfrac{AB^2}{DE^2}$
As we know, if two triangles are similar, ratio of their areas are equal to the square of the ratio of their corresponding sides
⇒ $\dfrac{AC^2}{DF^2} = \dfrac{BC^2}{EF^2}$
$\dfrac{64}{121} = \dfrac{BC^2}{EF^2}$
$(\dfrac{8}{11})^2 = (\dfrac{BC}{15.4})^2$
$\dfrac{8}{11} = \dfrac{BC}{15.4}$
BC = 8×$\dfrac{15.4}{11}$
BC = 8 × 1.4
BC = 11.2 cm
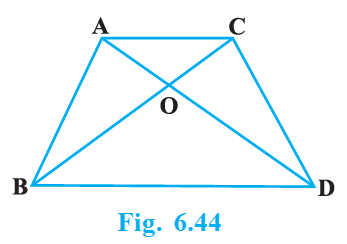
If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.
Given
ABCD is a trapezium with AB || DC. Diagonals AC and BD intersect each other at point O.

In ΔAOB and ΔCOD, we have
$\angle1 = \angle2$ (Alternate angles)
$\angle3 = \angle4$ (Alternate angles)
$\angle5 = \angle6$ (Vertically opposite angle)
∴ ΔAOB ~ ΔCOD [AAA similarity criterion]
As we know, If two triangles are similar then the ratio of their areas are equal to the square of the ratio of their corresponding sides.
Therefore,$\dfrac{Area \: of \: (ΔAOB)}{Area \: of \: (ΔCOD} = \dfrac{AB^2}{CD^2}$
= $\dfrac{(2CD)^2}{CD^2}$ [∴ AB = 2CD]
∴ $\dfrac{Area \: of \: (ΔAOB)}{Area \: of \: (ΔCOD)}$
= $\dfrac{4CD^2}{CD^2} = \dfrac{4}{1}$
Hence, the required ratio of the area of ΔAOB and ΔCOD = 4:1
Given,
ABC and DBC are two triangles on the same base BC. AD intersects BC at O
We have to prove:
$\dfrac{Area (ΔABC)}{Area (ΔDBC)}$ = $\dfrac{AO}{DO}$
Let us draw two perpendiculars AP and DM on line BC

We know that area of a triangle = $\dfrac{1}{2}$ × Base × Height
$\dfrac{ar (\triangle ABC)}{ar(\triangle DEF)} = \dfrac{\frac{1}{2}\times BC \times AP}{\frac{1}{2}\times BC \times DM} = \dfrac{AP}{DM}$
In ΔAPO and ΔDMO
$\angle APO = \angle DMO$ (Each 90°)
$\angle AOP = \angle DOM$ (Vertically opposite angles)
∴ ΔAPO ~ ΔDMO (AA similarity criterion)
∴$\dfrac{AP}{DM} = \dfrac{AO}{DO}$
$\dfrac{Area (ΔABC)}{Area (ΔDBC)} = \dfrac{AO}{DO}$
Say ΔABC and ΔPQR are two similar triangles and equal in area
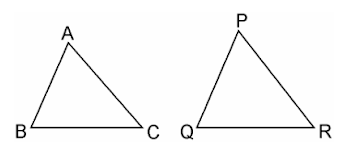
Now let us prove ΔABC ≅ ΔPQR.
Since, ΔABC ~ ΔPQR
$\dfrac{Area \: of \: (ΔABC)}{Area \: of \: (ΔPQR)} = \dfrac{BC^2}{QR^2}$
$\dfrac{BC^2}{QR^2} =1 [Since, Area(ΔABC) = (ΔPQR)$
$\dfrac{BC^2}{QR^2}$
BC = QR
Similarly, we can prove that
AB = PQ and AC = PR
Thus, ΔABC ≅ ΔPQR [SSS criterion of congruence]
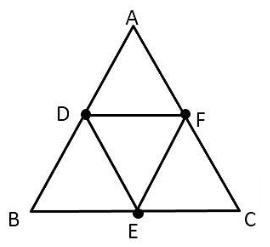
D, E, and F are the mid-points of ΔABC
DE || AC and
DE =$ \dfrac{1}{2}$ AC (Midpoint theorem) …. (1)
In ΔBED and ΔBCA
$\angle BED = \angle BCA$ (Corresponding angles)
$\angle BDE = \angle BAC$ (Corresponding angles)
$\angle EBD = \angle CBA$ (Common angles)
ΔBED∼ΔBCA (AAA similarity criterion)
$\dfrac{ar (ΔBED) }{ ar (ΔBCA)}=(\dfrac{DE}{AC})^2$
$\dfrac{ar (ΔBED) }{ ar (ΔBCA)} = \dfrac{1}{4}$ [From (1)]
ar (ΔBED) = $\dfrac{1}{4}$ ar (ΔBCA)
Similarly,
ar (ΔCFE) = $\dfrac{1}{4}$ ar (CBA) and ar (ΔADF) = $\dfrac{1}{4}$ ar (ΔADF) = $\dfrac{1}{4}$ ar (ΔABC)
Also,
ar (ΔDEF) = ar (ΔABC) − [ar (ΔBED) + ar (ΔCFE) + ar (ΔADF)]
ar (ΔDEF) = ar (ΔABC) − $\dfrac{3}{4}$ ar (ΔABC) = $\dfrac{1}{4}$ ar (ΔABC)
$\dfrac{ar (ΔDEF)}{ ar (ΔABC)} =\dfrac{1}{4}$
Given:
AM and DN are the medians of triangles ABC and DEF respectively and ΔABC ~ ΔDEF
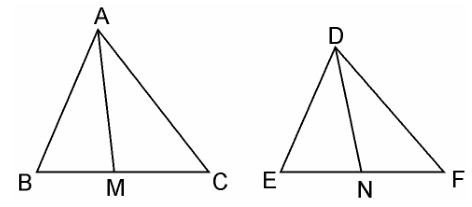
We have to prove: $\dfrac{Area(ΔABC)}{Area(ΔDEF)} = \dfrac{AM^2}{DN^2}$
Since, ΔABC ~ ΔDEF (Given)
$\dfrac{ Area(ΔABC)}{Area(ΔDEF)} = \dfrac{AB^2}{DE^2}$ ……………………………(i)
and,$\dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{CA}{FD} $………………………………………(ii)
$\dfrac{AB}{DE} = \dfrac{\frac{1}{2}\times BC}{\frac{1}{2}\times EF} = \dfrac{CD}{FD}$
In ΔABM and ΔDEN,
Since ΔABC ~ ΔDEF
$\angle B = \angle E$
$\dfrac{AB}{DE} = \dfrac{BM}{EN}$ [Already Proved in equation (i)]
ΔABC ~ ΔDEF [SAS similarity criterion] $\dfrac{AB}{DE} = \dfrac{AM}{DN}$ …………………………………………………..(iii)ΔABM ~ ΔDEN
As the areas of two similar triangles are proportional to the squares of the corresponding sides
$\dfrac{ area(ΔABC)}{area(ΔDEF)} = \dfrac{AB^2}{DE^2} = \dfrac{AM^2}{DN^2}$
Hence, proved
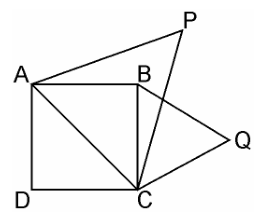
Given, ABCD is a square whose one diagonal is AC. ΔAPC and ΔBQC are two equilateral triangles described on the diagonals AC and side BC of the square ABCD.
Area(ΔBQC) = $\dfrac{1}{2}$ Area(ΔAPC)
Since, ΔAPC and ΔBQC are both equilateral triangles, as per given,
ΔAPC ~ ΔBQC [AAA similarity criterion]
$\dfrac{area(ΔAPC)}{area(ΔBQC)} = \dfrac{AC^2}{BC^2} = \dfrac{AC^2}{BC^2}$
Since, Diagonal = $\sqrt{2} side = \sqrt{2}$ BC = AC
area(ΔAPC) = 2 × area(ΔBQC)
area(ΔBQC) = $\dfrac{1}{2}$ area(ΔAPC)
Hence, proved
ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is
Given, ΔABC and ΔBDE are two equilateral triangle. D is the midpoint of BC.

∴ BD = DC = $\dfrac{1}{2BC}$
Let each side of triangle is 2a.
As, ΔABC ~ ΔBDE
$\dfrac{ Area(ΔABC)}{Area(ΔBDE)} = \dfrac{AB^2}{BD^2} = \dfrac{(2a)^2}{(a)^2} = \dfrac{4a^2}{a^2} = \dfrac{4}{1} = 4:1$
Hence, the correct answer is (C).
Given, Sides of two similar triangles are in the ratio 4 : 9

Let ABC and DEF are two similar triangles, such that,
ΔABC ~ ΔDEF
And $\dfrac{AB}{DE} = \dfrac{AC}{DF} = \dfrac{BC}{EF} = \dfrac{4}{9}$
As, the ratio of the areas of these triangles will be equal to the square of the ratio of the corresponding sides,
$\dfrac{ Area(ΔABC)}{Area(ΔDEF)} = \dfrac{AB^2}{DE^2}$
$\dfrac{ Area(ΔABC)}{Area(ΔDEF)} = (\dfrac{4}{9})^2 = \dfrac{16}{81}$ = 16:81
Hence, the correct answer is (D)
