Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of th

Question 6 Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

Solution:

Given:

AM and DN are the medians of triangles ABC and DEF respectively and ΔABC ~ ΔDEF

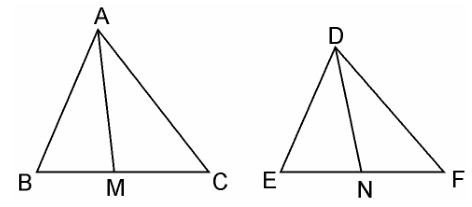
We have to prove: $\dfrac{Area(ΔABC)}{Area(ΔDEF)} = \dfrac{AM^2}{DN^2}$

Since, ΔABC ~ ΔDEF (Given)

$\dfrac{ Area(ΔABC)}{Area(ΔDEF)} = \dfrac{AB^2}{DE^2}$ ……………………………(i)

and,$\dfrac{AB}{DE} = \dfrac{BC}{EF} = \dfrac{CA}{FD} $………………………………………(ii)

$\dfrac{AB}{DE} = \dfrac{\frac{1}{2}\times BC}{\frac{1}{2}\times EF} = \dfrac{CD}{FD}$

In ΔABM and ΔDEN,

Since ΔABC ~ ΔDEF

$\angle B = \angle E$

$\dfrac{AB}{DE} = \dfrac{BM}{EN}$ [Already Proved in equation (i)]

ΔABC ~ ΔDEF [SAS similarity criterion]

$\dfrac{AB}{DE} = \dfrac{AM}{DN}$ …………………………………………………..(iii)

ΔABM ~ ΔDEN

As the areas of two similar triangles are proportional to the squares of the corresponding sides

$\dfrac{ area(ΔABC)}{area(ΔDEF)} = \dfrac{AB^2}{DE^2} = \dfrac{AM^2}{DN^2}$

Hence, proved

Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.	Answer
Tick the correct answer and justify : ABC and BDE are two equilateral triangles such that D is the mid-point of BC. Ratio of the areas of triangles ABC and BDE is	Answer
Sides of two similar triangles are in the ratio 4 : 9. Areas of these triangles are in the ratio	Answer
Let Δ ABC ~ Δ DEF and their areas be, respectively, $64 cm^2$ and $121 cm^2$. If EF = 15.4 cm, find BC.	Answer
Diagonals of a trapezium ABCD with AB \|\| DC intersect each other at the point O. If AB = 2 CD, find the ratio of the areas of triangles AOB and COD.	Answer
In Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that $\dfrac{ar (ABC)}{ar (DBC)} = \dfrac {AO}{DO}$		Answer
If the areas of two similar triangles are equal, prove that they are congruent.	Answer
D, E and F are respectively the mid-points of sides AB, BC and CA of Δ ABC. Find the ratio of the areas of Δ DEF and Δ ABC.	Answer
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.	Answer
Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.	Answer