 |
 |
 |
 |
 |
 |
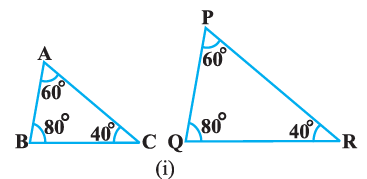
| i) Given, in ΔABC and ΔPQR, $\angle A = \angle P = 60°$ $\angle B = \angle Q = 80°$ $\angle C = \angle R = 40°$ Therefore by AAA similarity criterion, ∴ ΔABC ~ ΔPQR |  |
|
(ii) Given, in ΔABC and ΔPQR, $\dfrac{AB}{QR} = \dfrac{2}{4} = \dfrac{1}{2}$ $\dfrac{BC}{RP} = \dfrac{2.5}{5} = \dfrac{1}{2}$ $\dfrac{CA}{PA} = \dfrac{3}{6} = \dfrac{1}{2}$ By SSS similarity criterion, ΔABC ~ ΔQRP |  |
|
(iii) Given, in ΔLMP and ΔDEF LM = 2.7, MP = 2, LP = 3, EF = 5, DE = 4, DF = 6 $\dfrac{MP}{DE} = \dfrac{2}{4} = \dfrac{1}{2}$ $\dfrac{PL}{DF} = \dfrac{3}{6} = \dfrac{1}{2}$ $\dfrac{LM}{EF} = \dfrac{2.7}{5} = \dfrac{27}{50}$ Since the ratios are not same $\dfrac{MP}{DE} = \dfrac{PL}{DF} ≠ \dfrac{LM}{EF}$ Therefore, ΔLMP and ΔDEF are not similar. |  |
|
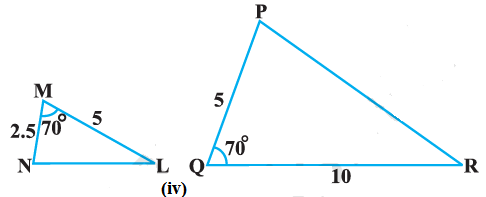
(iv) In ΔMNL and ΔQPR, it is given, $\dfrac{MN}{QP} = \dfrac{ML}{QR} = \dfrac{1}{2}$ $\angle M = \angle Q = 70°$ Therefore, by SAS similarity criterion ∴ ΔMNL ~ ΔQPR |  |
|
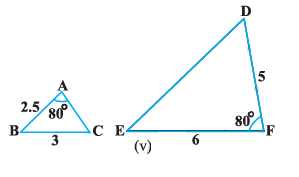
(v) In ΔABC and ΔDEF, given that, AB = 2.5, BC = 3, $\angle A = 80°, EF = 6, DF = 5, \angle F = 80°$ Here , $\dfrac{AB}{DF} = \dfrac{2.5}{5} = \dfrac{1}{2}$ And, $\dfrac{BC}{EF} = \dfrac{3}{6} = \dfrac{1}{2}$ $\angle B ≠ \angle F$ Hence, ΔABC and ΔDEF are not similar. |  |
|
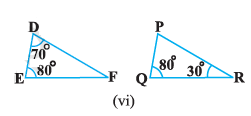
(vi) Given ΔDEF and PQR in ΔDEF ,by sum of angles of triangles, we know that, $\angle D + \angle E + \angle F = 180°$ 70° + 80° + $\angle F = 180°$ $\angle F = 180° – 70° – 80°$ $\angle F = 30°$ Similarly, In ΔPQR, $\angle P + \angle Q + \angle R = 180$ (Sum of angles of Δ) $\angle P + 80° + 30° = 180°$ $\angle P = 180° – 80° -30°$ $\angle P = 70°$ Now, comparing both the triangles, ΔDEF and ΔPQR, we have $\angle D = \angle P = 70°$ $\angle F = \angle Q = 80°$ $\angle F = \angle R = 30°$ Therefore, by AAA similarity criterion, Hence, ΔDEF ~ ΔPQR |  |

From the given figure, DOB is a straight line.
$\angle DOC + \angle COB = 180°$
$\angle DOC$ = 180° – 125° (Given, $\angle BOC = 125°$) = 55°
Now in ΔDOC,
Sum of the measures of the angles of a triangle is 180º
$\angle DCO + \angle CDO + \angle DOC = 180°$
$\angle DCO + 70º + 55º = 180°$(Given, $\angle CDO = 70°$)
$\angle DCO = 180° - 125º = 55°$
It is given that, ΔODC ~ ΔOBA,
$\angle OAB = \angle OCD = 55°$
$\angle DOC = 55°, \angle DCO = 55°, \angle OAB = 55$
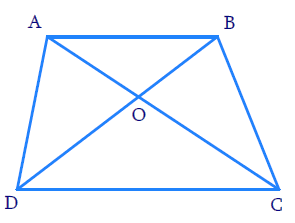
In ΔDOC and ΔBOA,
AB || CD, thus alternate interior angles will be equal,
$\angle CDO = \angle ABO$
Similarly,
$\angle DCO = \angle BAO$
Also, for the two triangles ΔDOC and ΔBOA, vertically opposite angles will be equal;
$\angle DOC = \angle BOA$
Hence, by AAA similarity criterion,
ΔDOC ~ ΔBOA
Thus, the corresponding sides are proportional.
$\dfrac{DO}{BO} = \dfrac{OC}{OA}$
$\dfrac{OA}{OC} = \dfrac{OB}{OD}$
Hence, proved.

In ΔPQR,
$\angle PQR = \angle PRQ$
∴ PQ = PR ………………………(i)
Given,
$ \dfrac{QR}{QS} = \dfrac{QT}{PR}$ Using equation (i), we get
$\dfrac{QR}{QS} = \dfrac{QT}{QP}$……………….(ii)
In ΔPQS and ΔTQR, by equation (ii),
$\dfrac{QR}{QS} = \dfrac{QT}{QP}$
$\angle Q = \angle Q$
∴ ΔPQS ~ ΔTQR [By SAS similarity criterion]
Given, S and T are point on sides PR and QR of ΔPQR
And $\angle P = \angle RTS$

In ΔRPQ and ΔRTS,
$\angle RTS = \angle QPS $(Given)
$\angle R = \angle R $(Common angle)
∴ ΔRPQ ~ ΔRTS (AA similarity criterion)
Given, ΔABE ≅ ΔACD
∴ AB = AC [By (CPCT)] ……………………………….(i)
And, AD = AE [By (CPCT)] ……………………………(ii)
(CPCT - Corresponding parts of congruent triangle)
In ΔADE and ΔABC, dividing equation (ii) by (i)
$ \dfrac{AD}{AB} = \dfrac{AE}{AC}$
$\angle A = \angle A $ [Common angle]
ΔADE ~ ΔABC [SAS similarity criterion]
|
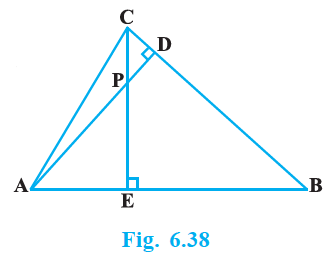
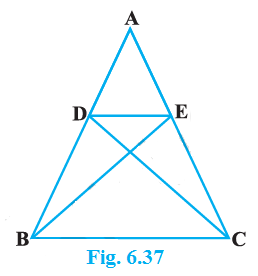
(i) Δ AEP ~ Δ CDP (ii) Δ ABD ~ Δ CBE (iii) Δ AEP ~ Δ ADB (iv) Δ PDC ~ Δ BEC |
|
Given, altitudes AD and CE of ΔABC intersect each other at the point P.
(i) In ΔAEP and ΔCDP
$\angle AEP = \angle CDP $(90° each)
$\angle APE = \angle CPD $(Vertically opposite angles)
Hence, by AA similarity criterion
ΔAEP ~ ΔCDP
(ii) In ΔABD and ΔCBE
$\angle ADB = \angle CEB$ ( 90° each)
$\angle ABD = \angle CBE$ (Common Angles)
Hence, by AA similarity criterion
ΔABD ~ ΔCBE
(iii) In ΔAEP and ΔADB
$\angle AEP = \angle ADB$ (90° each)
$\angle PAE = \angle DAB$ (Common Angles)
Hence, by AA similarity criterion,
ΔAEP ~ ΔADB
(iv) In ΔPDC and ΔBEC
$\angle PDC = \angle BEC$ (90° each)
$\angle PCD = \angle BCE$ (Common angles)
Hence, by AA similarity criterion,
ΔPDC ~ ΔBEC
Given, E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Consider the figure below
In ΔABE and ΔCFB
$\angle A = \angle C$ (Opposite angles of a parallelogram)
$\angle AEB = \angle CBF$ (Alternate interior angles as AE || BC)
ΔABE ~ ΔCFB (AA similarity criterion)
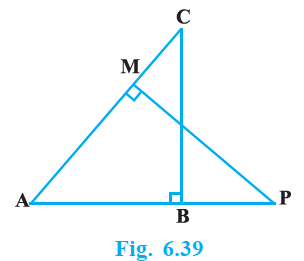
(i) Δ ABC ~ Δ AMP (ii) $\dfrac{CA}{PA} = \dfrac{BC}{MP}$ |
|
Given, ABC and AMP are two right triangles, right angled at B and M respectively.
(i) In ΔABC and ΔAMP, we have
$\angle CAB = \angle MAP$ (common angles)
$\angle ABC = \angle AMP = 90°$ (each 90°)
ΔABC ~ ΔAMP (AA similarity criterion)
(ii) As, ΔABC ~ ΔAMP (AA similarity criterion)
If two triangles are similar then the corresponding sides are always equal
Hence, $\dfrac{CA}{PA} = \dfrac{BC}{MP}$
(i)$\dfrac{CD}{GH} = \dfrac{AC}{FG}$
(ii) Δ DCB ~ Δ HGE
(iii) Δ DCA ~ Δ HGF
Given, CD and GH are respectively the bisectors of $\angle ACB$ and $\angle EGF$ such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively.
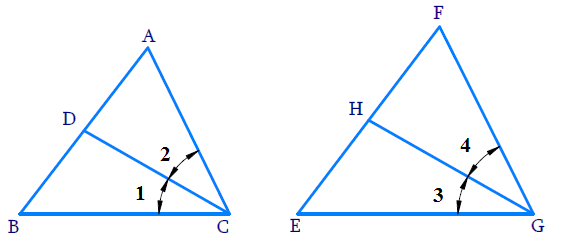
(i) From the given condition, ΔABC ~ ΔFEG
$\angle A = \angle F, \angle B = \angle E, and \angle ACB = \angle FGE$
Since, $\angle ACB = \angle FGE$
$\angle ACD = \angle FGH$ (Angle bisector)
And, $\angle DCB = \angle HGE$ (Angle bisector)
In ΔACD and ΔFGH
$\angle A = \angle F$
$\angle ACD = \angle FGH$
ΔACD ~ ΔFGH (AA similarity criterion)
$\dfrac{CD}{GH} = \dfrac{AC}{FG}$
(ii) In ΔDCB and ΔHGE
$\angle DCB = \angle HGE$ (Already proved)
$\angle B = \angle E$ (Already proved)
ΔDCB ~ ΔHGE (AA similarity criterion)
(iii) In ΔDCA and ΔHGF
$\angle ACD = \angle FGH$ (Already proved)
$\angle A = \angle F$ (Already proved)
ΔDCA ~ ΔHGF (AA similarity criterion)