Question 10
CD and GH are respectively the bisectors of $\angle ACB$ and $\angle EGF$ such that D and H lie on sides AB and FE of Δ ABC and Δ EFG respectively. If Δ ABC ~ Δ FEG, show that:
(i)$\dfrac{CD}{GH} = \dfrac{AC}{FG}$
(ii) Δ DCB ~ Δ HGE
(iii) Δ DCA ~ Δ HGF
(i)$\dfrac{CD}{GH} = \dfrac{AC}{FG}$
(ii) Δ DCB ~ Δ HGE
(iii) Δ DCA ~ Δ HGF
Solution:
Given, CD and GH are respectively the bisectors of $\angle ACB$ and $\angle EGF$ such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively.
Given, CD and GH are respectively the bisectors of $\angle ACB$ and $\angle EGF$ such that D and H lie on sides AB and FE of ΔABC and ΔEFG respectively.
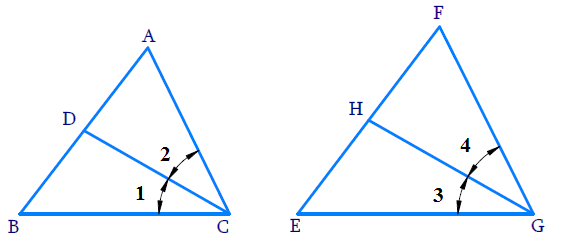
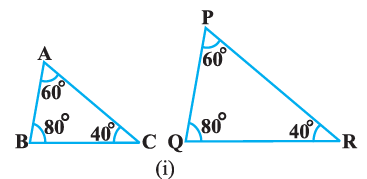
(i) From the given condition, ΔABC ~ ΔFEG
$\angle A = \angle F, \angle B = \angle E, and \angle ACB = \angle FGE$
Since, $\angle ACB = \angle FGE$
$\angle ACD = \angle FGH$ (Angle bisector)
And, $\angle DCB = \angle HGE$ (Angle bisector)
In ΔACD and ΔFGH
$\angle A = \angle F$
$\angle ACD = \angle FGH$
ΔACD ~ ΔFGH (AA similarity criterion)
$\dfrac{CD}{GH} = \dfrac{AC}{FG}$
(ii) In ΔDCB and ΔHGE
$\angle DCB = \angle HGE$ (Already proved)
$\angle B = \angle E$ (Already proved)
ΔDCB ~ ΔHGE (AA similarity criterion)
(iii) In ΔDCA and ΔHGF
$\angle ACD = \angle FGH$ (Already proved)
$\angle A = \angle F$ (Already proved)
ΔDCA ~ ΔHGF (AA similarity criterion)
