A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower cas

For Competitive Exams

Question 15 A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.

Solution:

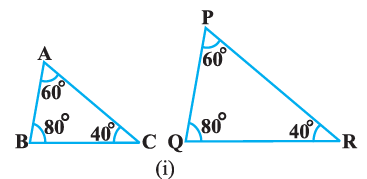
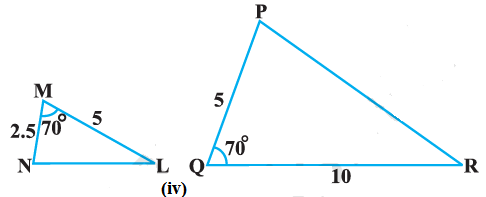
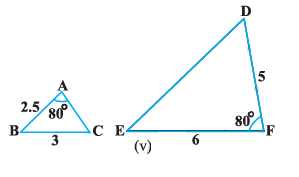
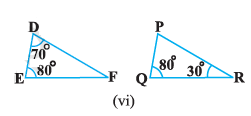
Given,

Length of the vertical pole = 6m

Shadow of the pole = 4 m

Let Height of tower = h m

Length of shadow of the tower = 28 m

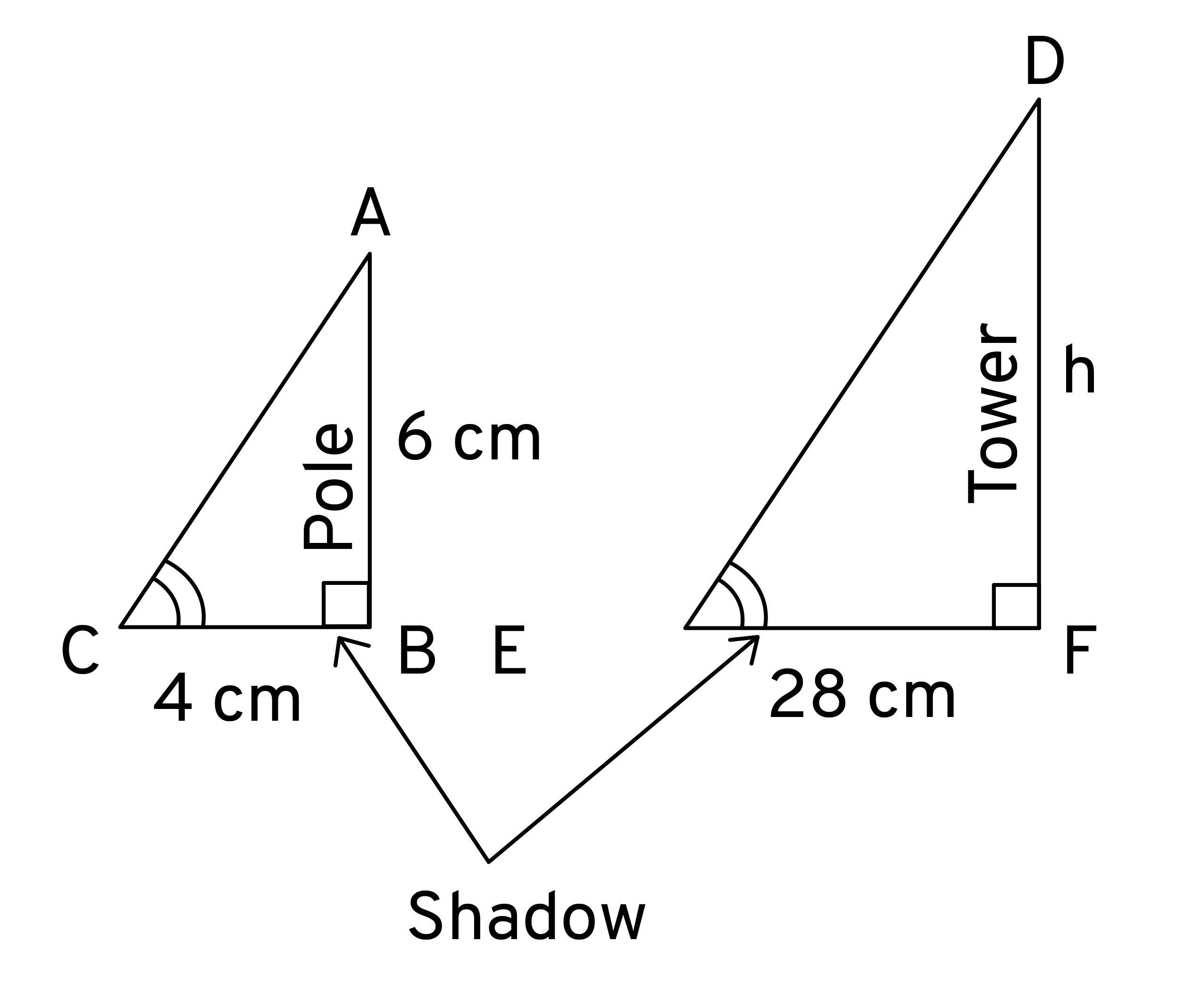
In ΔABC and ΔDEF

$\angle C = \angle E$ (angular elevation of sum)

$\angle B = \angle F = 90°$

ΔABC ~ ΔDEF (AA similarity criterion)

$\dfrac{AB}{DF} = \dfrac{BC}{EF}$ (If two triangles are similar corresponding sides are proportional)

$\dfrac{6}{h} = \dfrac{4}{28}$

$h = \dfrac{(6×28)}{4}$

h = 6 × 7

h = 42 m

Hence, the height of the tower is 42 m.

Additional Questions

If AD and PM are medians of triangles ABC and PQR, respectively where Δ ABC ~ Δ PQR, prove that $\dfrac{AB}{PQ} = \dfrac{AD}{PM}$

Answer

State which pairs of triangles in Fig are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :

Answer

In Fig 6.35, Δ ODC ~ Δ OBA, $\angle BOC = 125°$ and $\angle CDO = 70°$. Find $\angle DOC, \angle DCO$ and $\angle OAB$.

Answer

Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that $\dfrac{OA}{OC} = \dfrac{OB}{OD}$

Answer

In Fig. 6.36, $\dfrac{QR}{QS} = \dfrac{QT}{PR}$ and $ \angle 1 = \angle 2$. Show that Δ PQS ~ Δ TQR.

Answer

S and T are points on sides PR and QR of Δ PQR such that $\angle P = \angle RTS$. Show that Δ RPQ ~ Δ RTS.

Answer

In Fig. 6.37, if Δ ABE ≅ Δ ACD, show that Δ ADE ~ Δ ABC.

Answer

In Fig. 6.38, altitudes AD and CE of Δ ABC intersect each other at the point P. Show that:

(i) Δ AEP ~ Δ CDP

(ii) Δ ABD ~ Δ CBE

(iii) Δ AEP ~ Δ ADB

(iv) Δ PDC ~ Δ BEC

Answer

E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that Δ ABE ~ Δ CFB.

Answer

In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:

(i) Δ ABC ~ Δ AMP

(ii) $\dfrac{CA}{PA} = \dfrac{BC}{MP}$

Answer

Share with Friends