If AD and PM are medians of triangles ABC and PQR, respectively where Δ ABC ~ Δ PQR, prove that \df

For Competitive Exams

Question 16 If AD and PM are medians of triangles ABC and PQR, respectively where Δ ABC ~ Δ PQR, prove that $\dfrac{AB}{PQ} = \dfrac{AD}{PM}$

Solution:

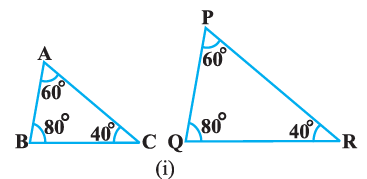
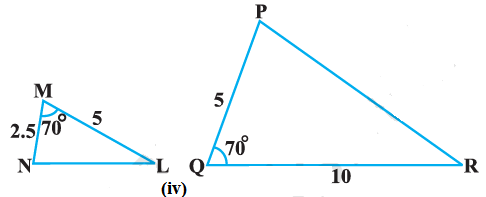
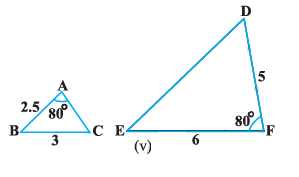
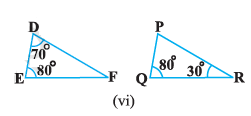
Given, ΔABC ~ ΔPQR

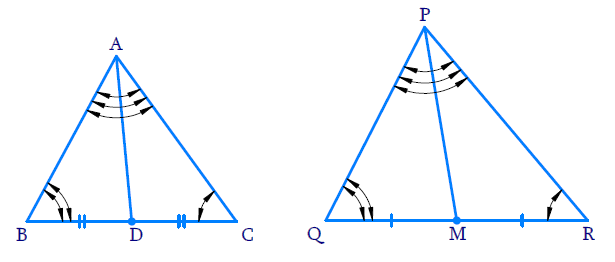
We know that the corresponding sides of similar triangles are in proportion.

$\dfrac{AB}{PQ} = \dfrac{AC}{PR} = \dfrac{BC}{QR} $……………………………(i)

Also, $\angle A = \angle P, \angle B = \angle Q, \angle C = \angle R $………….…..(ii)

Since AD and PM are medians, they will divide their opposite sides.

$BD = \dfrac{BC}{2}$ and $QM = \dfrac{QR}{2} $……………..………….(iii)

From equations (i) and (iii), we get

$\dfrac{AB}{PQ} = \dfrac{BD}{QM} $……………………….(iv)

In ΔABD and ΔPQM

From equation (ii), we have

$\angle B = \angle Q$

From equation (iv), we have

$\dfrac{AB}{PQ} = \dfrac{BD}{QM}$

ΔABD ~ ΔPQM (SAS similarity criterion)

$\dfrac{AB}{PQ} = \dfrac{BD}{QM} = \dfrac{AD}{PM}$

Additional Questions

State which pairs of triangles in Fig are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :

Answer

In Fig 6.35, Δ ODC ~ Δ OBA, $\angle BOC = 125°$ and $\angle CDO = 70°$. Find $\angle DOC, \angle DCO$ and $\angle OAB$.

Answer

Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that $\dfrac{OA}{OC} = \dfrac{OB}{OD}$

Answer

In Fig. 6.36, $\dfrac{QR}{QS} = \dfrac{QT}{PR}$ and $ \angle 1 = \angle 2$. Show that Δ PQS ~ Δ TQR.

Answer

S and T are points on sides PR and QR of Δ PQR such that $\angle P = \angle RTS$. Show that Δ RPQ ~ Δ RTS.

Answer

In Fig. 6.37, if Δ ABE ≅ Δ ACD, show that Δ ADE ~ Δ ABC.

Answer

In Fig. 6.38, altitudes AD and CE of Δ ABC intersect each other at the point P. Show that:

(i) Δ AEP ~ Δ CDP

(ii) Δ ABD ~ Δ CBE

(iii) Δ AEP ~ Δ ADB

(iv) Δ PDC ~ Δ BEC

Answer

E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that Δ ABE ~ Δ CFB.

Answer

In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:

(i) Δ ABC ~ Δ AMP

(ii) $\dfrac{CA}{PA} = \dfrac{BC}{MP}$

Answer

CD and GH are respectively the bisectors of $\angle ACB$ and $\angle EGF$ such that D and H lie on sides AB and FE of Δ ABC and Δ EFG respectively. If Δ ABC ~ Δ FEG, show that:
(i)$\dfrac{CD}{GH} = \dfrac{AC}{FG}$
(ii) Δ DCB ~ Δ HGE
(iii) Δ DCA ~ Δ HGF

Answer

Share with Friends