Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a s

For Competitive Exams

Question 3 Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that $\dfrac{OA}{OC} = \dfrac{OB}{OD}$

Solution:

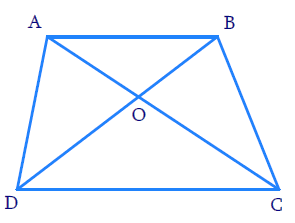
In ΔDOC and ΔBOA,

AB || CD, thus alternate interior angles will be equal,

$\angle CDO = \angle ABO$

Similarly,

$\angle DCO = \angle BAO$

Also, for the two triangles ΔDOC and ΔBOA, vertically opposite angles will be equal;

$\angle DOC = \angle BOA$

Hence, by AAA similarity criterion,

ΔDOC ~ ΔBOA

Thus, the corresponding sides are proportional.

$\dfrac{DO}{BO} = \dfrac{OC}{OA}$

$\dfrac{OA}{OC} = \dfrac{OB}{OD}$

Hence, proved.

Additional Questions

In Fig. 6.36, $\dfrac{QR}{QS} = \dfrac{QT}{PR}$ and $ \angle 1 = \angle 2$. Show that Δ PQS ~ Δ TQR.

Answer

S and T are points on sides PR and QR of Δ PQR such that $\angle P = \angle RTS$. Show that Δ RPQ ~ Δ RTS.

Answer

In Fig. 6.37, if Δ ABE ≅ Δ ACD, show that Δ ADE ~ Δ ABC.

Answer

In Fig. 6.38, altitudes AD and CE of Δ ABC intersect each other at the point P. Show that:

(i) Δ AEP ~ Δ CDP

(ii) Δ ABD ~ Δ CBE

(iii) Δ AEP ~ Δ ADB

(iv) Δ PDC ~ Δ BEC

Answer

E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that Δ ABE ~ Δ CFB.

Answer

In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:

(i) Δ ABC ~ Δ AMP

(ii) $\dfrac{CA}{PA} = \dfrac{BC}{MP}$

Answer

CD and GH are respectively the bisectors of $\angle ACB$ and $\angle EGF$ such that D and H lie on sides AB and FE of Δ ABC and Δ EFG respectively. If Δ ABC ~ Δ FEG, show that:
(i)$\dfrac{CD}{GH} = \dfrac{AC}{FG}$
(ii) Δ DCB ~ Δ HGE
(iii) Δ DCA ~ Δ HGF

Answer

In Fig. 6.40, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that Δ ABD ~ Δ ECF.

Answer

Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of Δ PQR (see Fig. 6.41). Show that Δ ABC ~ Δ PQR.

Answer

D is a point on the side BC of a triangle ABC such that $\angle ADC = \angle BAC$. Show that $CA^2$ = CB.CD.

Answer

Share with Friends