Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and

For Competitive Exams

10th CBSE Maths

Question 12 Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of Δ PQR (see Fig. 6.41). Show that Δ ABC ~ Δ PQR.

Solution:

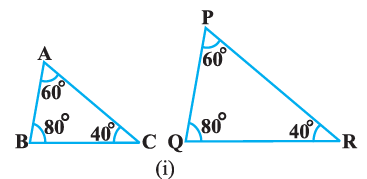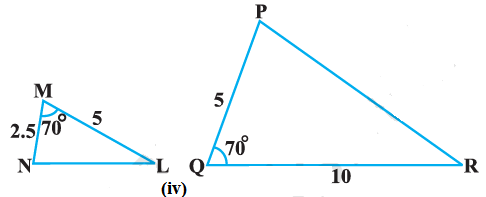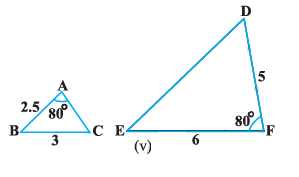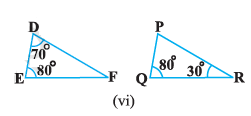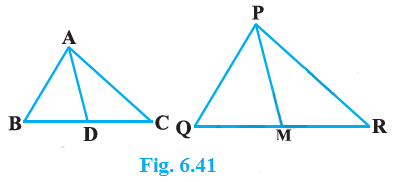
Given

ΔABC and ΔPQR, AB, BC and median AD of ΔABC are proportional to sides PQ, QR and median PM of ΔPQR

$\dfrac{AB}{PQ} = \dfrac{BC}{QR} = \dfrac{AD}{PM}$

We have to prove: ΔABC ~ ΔPQR

As we know here

$\dfrac{AB}{PQ} = \dfrac{BC}{QR} = \dfrac{AD}{PM}$

or $\dfrac{AB}{PQ} = \dfrac{(\dfrac{1}{2})BC}{(\dfrac{1}{2})QR} = \dfrac{AD}{PM}$

$\dfrac{AB}{PQ} = \dfrac{BC}{QR} = \dfrac{AD}{PM}$ (D is the midpoint of BC. M is the midpoint of QR)

ΔABD ~ ΔPQM [SSS similarity criterion]

$\angle ABD = \angle $PQM [Corresponding angles of two similar triangles are equal]

$\angle ABC = \angle PQR$

In ΔABC and ΔPQR

$\dfrac{AB}{PQ} = \dfrac{BC}{QR}$ ………………………….(i)

$\angle ABC = \angle PQR$ ……………………………(ii)

From equation (i) and (ii), we get

ΔABC ~ ΔPQR [SAS similarity criterion]

Additional Questions

D is a point on the side BC of a triangle ABC such that $\angle ADC = \angle BAC$. Show that $CA^2$ = CB.CD.

Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that Δ ABC ~ Δ PQR.

A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts a shadow 28 m long. Find the height of the tower.

If AD and PM are medians of triangles ABC and PQR, respectively where Δ ABC ~ Δ PQR, prove that $\dfrac{AB}{PQ} = \dfrac{AD}{PM}$

State which pairs of triangles in Fig are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :

In Fig 6.35, Δ ODC ~ Δ OBA, $\angle BOC = 125°$ and $\angle CDO = 70°$. Find $\angle DOC, \angle DCO$ and $\angle OAB$.

Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that $\dfrac{OA}{OC} = \dfrac{OB}{OD}$

In Fig. 6.36, $\dfrac{QR}{QS} = \dfrac{QT}{PR}$ and $ \angle 1 = \angle 2$. Show that Δ PQS ~ Δ TQR.

S and T are points on sides PR and QR of Δ PQR such that $\angle P = \angle RTS$. Show that Δ RPQ ~ Δ RTS.

In Fig. 6.37, if Δ ABE ≅ Δ ACD, show that Δ ADE ~ Δ ABC.

Share with Friends

Privacy Copyright Contact Us