Solution:

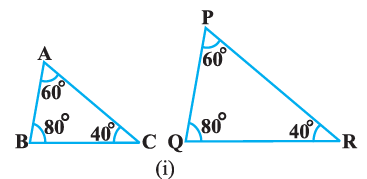
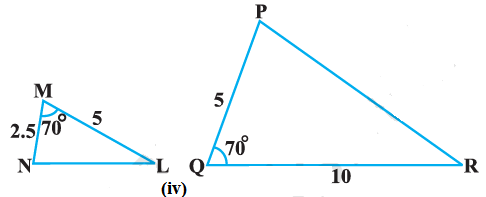
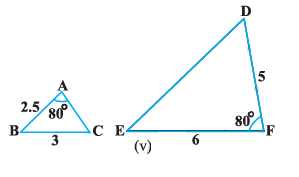
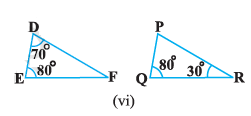
Given,

Two triangles ΔABC and ΔPQR in which AD and PM are medians such that

$\dfrac{AB}{PQ} = \dfrac{AC}{PR} = \dfrac{AD}{PM}$

We have to prove, ΔABC ~ ΔPQR

Let us construct first

Produce AD to E so that AD = DE. Join CE, Similarly produce PM to N such that PM = MN, also Join RN.

In ΔABD and ΔCDE, we have

AD = DE [By Construction.]

BD = DC [Since, AP is the median]

and, $\angle ADB = \angle CDE$ [Vertically opposite angles]

ΔABD ≅ ΔCDE [SAS criterion of congruence]

AB = CE [By CPCT] …………………………..(i)

Also, in ΔPQM and ΔMNR

PM = MN [By Construction]

QM = MR [Since, PM is the median]

and, $\angle PMQ = \angle NMR $[Vertically opposite angles]

ΔPQM = ΔMNR [SAS criterion of congruence]

PQ = RN [CPCT] ………………………………(ii)

Now, $\dfrac{AB}{PQ} = \dfrac{AC}{PR} = \dfrac{AD}{PM}$

From equation (i) and (ii)

$\dfrac{CE}{RN} = \dfrac{AC}{PR} = \dfrac{AD}{PM}$

$\dfrac{CE}{RN} = \dfrac{AC}{PR} = \dfrac{2AD}{2PM}$

$\dfrac{CE}{RN} = \dfrac{AC}{PR} = \dfrac{AE}{PN}$ [Since 2AD = AE and 2PM = PN]

ΔACE ~ ΔPRN [SSS similarity criterion]

Therefore,$ \angle 2 = \angle 4$

Similarly,$ \angle 1 = \angle 3$

$\angle 1 + \angle 2 = \angle 3 + \angle 4$

$\angle A = \angle P$ …………………………………………….(iii)

Now, in ΔABC and ΔPQR, we have

$\dfrac{AB}{PQ} = \dfrac{AC}{PR}$ (Already given)

From equation (iii)

$\angle A = \angle P$

ΔABC ~ ΔPQR [ SAS similarity criterion]