Easy Tutorial
For Competitive Exams
Aptitude
TNPSC G4
10th CBSE Maths
  1. Home
  2. CBSE 10th Maths
  3. Triangles
  4. Exercise 6.3
  5. Q:1
Question 1 State which pairs of triangles in Fig are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form :
Solution:

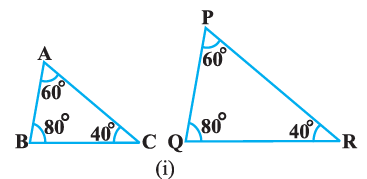
i) Given, in ΔABC and ΔPQR,

$\angle A = \angle P = 60°$

$\angle B = \angle Q = 80°$

$\angle C = \angle R = 40°$

Therefore by AAA similarity criterion,

∴ ΔABC ~ ΔPQR

(ii) Given, in ΔABC and ΔPQR,

$\dfrac{AB}{QR} = \dfrac{2}{4} = \dfrac{1}{2}$

$\dfrac{BC}{RP} = \dfrac{2.5}{5} = \dfrac{1}{2}$

$\dfrac{CA}{PA} = \dfrac{3}{6} = \dfrac{1}{2}$

By SSS similarity criterion,

ΔABC ~ ΔQRP

(iii) Given, in ΔLMP and ΔDEF

LM = 2.7, MP = 2, LP = 3, EF = 5, DE = 4, DF = 6

$\dfrac{MP}{DE} = \dfrac{2}{4} = \dfrac{1}{2}$

$\dfrac{PL}{DF} = \dfrac{3}{6} = \dfrac{1}{2}$

$\dfrac{LM}{EF} = \dfrac{2.7}{5} = \dfrac{27}{50}$

Since the ratios are not same

$\dfrac{MP}{DE} = \dfrac{PL}{DF} ≠ \dfrac{LM}{EF}$

Therefore, ΔLMP and ΔDEF are not similar.

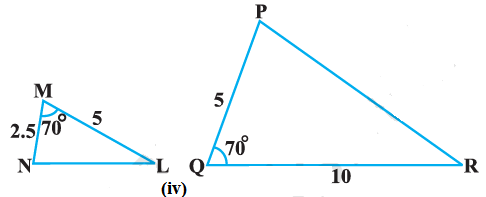
(iv) In ΔMNL and ΔQPR, it is given,

$\dfrac{MN}{QP} = \dfrac{ML}{QR} = \dfrac{1}{2}$

$\angle M = \angle Q = 70°$

Therefore, by SAS similarity criterion

∴ ΔMNL ~ ΔQPR

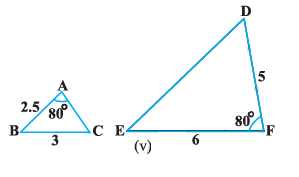
(v) In ΔABC and ΔDEF, given that,

AB = 2.5, BC = 3, $\angle A = 80°, EF = 6, DF = 5, \angle F = 80°$

Here , $\dfrac{AB}{DF} = \dfrac{2.5}{5} = \dfrac{1}{2}$

And, $\dfrac{BC}{EF} = \dfrac{3}{6} = \dfrac{1}{2}$

$\angle B ≠ \angle F$

Hence, ΔABC and ΔDEF are not similar.

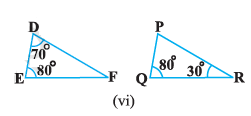
(vi) Given ΔDEF and PQR

in ΔDEF ,by sum of angles of triangles, we know that,

$\angle D + \angle E + \angle F = 180°$

70° + 80° + $\angle F = 180°$

$\angle F = 180° – 70° – 80°$

$\angle F = 30°$

Similarly, In ΔPQR,

$\angle P + \angle Q + \angle R = 180$ (Sum of angles of Δ)

$\angle P + 80° + 30° = 180°$

$\angle P = 180° – 80° -30°$

$\angle P = 70°$

Now, comparing both the triangles, ΔDEF and ΔPQR, we have

$\angle D = \angle P = 70°$

$\angle F = \angle Q = 80°$

$\angle F = \angle R = 30°$

Therefore, by AAA similarity criterion,

Hence, ΔDEF ~ ΔPQR
Additional Questions

In Fig 6.35, Δ ODC ~ Δ OBA, $\angle BOC = 125°$ and $\angle CDO = 70°$. Find $\angle DOC, \angle DCO$ and $\angle OAB$.

Answer

Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that $\dfrac{OA}{OC} = \dfrac{OB}{OD}$

Answer

In Fig. 6.36, $\dfrac{QR}{QS} = \dfrac{QT}{PR}$ and $ \angle 1 = \angle 2$. Show that Δ PQS ~ Δ TQR.

Answer

S and T are points on sides PR and QR of Δ PQR such that $\angle P = \angle RTS$. Show that Δ RPQ ~ Δ RTS.

 Answer

In Fig. 6.37, if Δ ABE ≅ Δ ACD, show that Δ ADE ~ Δ ABC.

Answer

In Fig. 6.38, altitudes AD and CE of Δ ABC intersect each other at the point P. Show that:

(i) Δ AEP ~ Δ CDP

(ii) Δ ABD ~ Δ CBE

(iii) Δ AEP ~ Δ ADB

(iv) Δ PDC ~ Δ BEC

Answer

E is a point on the side AD produced of a parallelogram ABCD and BE intersects CD at F. Show that Δ ABE ~ Δ CFB.

 Answer

In Fig. 6.39, ABC and AMP are two right triangles, right angled at B and M respectively. Prove that:

(i) Δ ABC ~ Δ AMP

(ii) $\dfrac{CA}{PA} = \dfrac{BC}{MP}$

Answer

CD and GH are respectively the bisectors of $\angle ACB$ and $\angle EGF$ such that D and H lie on sides AB and FE of Δ ABC and Δ EFG respectively. If Δ ABC ~ Δ FEG, show that:
(i)$\dfrac{CD}{GH} = \dfrac{AC}{FG}$
(ii) Δ DCB ~ Δ HGE
(iii) Δ DCA ~ Δ HGF

 Answer

In Fig. 6.40, E is a point on side CB produced of an isosceles triangle ABC with AB = AC. If AD ⊥ BC and EF ⊥ AC, prove that Δ ABD ~ Δ ECF.

Answer
Share with Friends
Privacy Copyright Contact Us