Question 7
In Fig. 6.38, altitudes AD and CE of Δ ABC intersect each other at the point P. Show that:
|
(i) Δ AEP ~ Δ CDP (ii) Δ ABD ~ Δ CBE (iii) Δ AEP ~ Δ ADB (iv) Δ PDC ~ Δ BEC |
|
Solution:
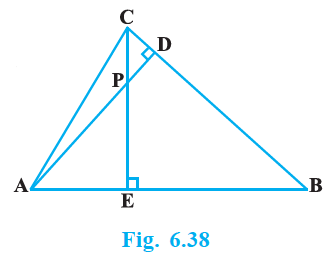
Given, altitudes AD and CE of ΔABC intersect each other at the point P.
(i) In ΔAEP and ΔCDP
$\angle AEP = \angle CDP $(90° each)
$\angle APE = \angle CPD $(Vertically opposite angles)
Hence, by AA similarity criterion
ΔAEP ~ ΔCDP
(ii) In ΔABD and ΔCBE
$\angle ADB = \angle CEB$ ( 90° each)
$\angle ABD = \angle CBE$ (Common Angles)
Hence, by AA similarity criterion
ΔABD ~ ΔCBE
(iii) In ΔAEP and ΔADB
$\angle AEP = \angle ADB$ (90° each)
$\angle PAE = \angle DAB$ (Common Angles)
Hence, by AA similarity criterion,
ΔAEP ~ ΔADB
(iv) In ΔPDC and ΔBEC
$\angle PDC = \angle BEC$ (90° each)
$\angle PCD = \angle BCE$ (Common angles)
Hence, by AA similarity criterion,
ΔPDC ~ ΔBEC
