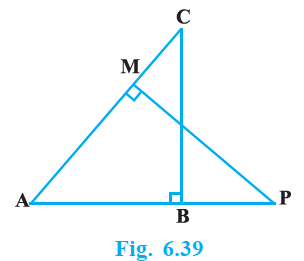
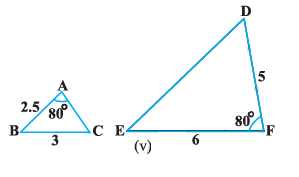
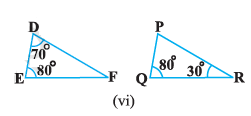
(i) Δ ABC ~ Δ AMP (ii) $\dfrac{CA}{PA} = \dfrac{BC}{MP}$ |
|
Given, ABC and AMP are two right triangles, right angled at B and M respectively.
(i) In ΔABC and ΔAMP, we have
$\angle CAB = \angle MAP$ (common angles)
$\angle ABC = \angle AMP = 90°$ (each 90°)
ΔABC ~ ΔAMP (AA similarity criterion)
(ii) As, ΔABC ~ ΔAMP (AA similarity criterion)
If two triangles are similar then the corresponding sides are always equal
Hence, $\dfrac{CA}{PA} = \dfrac{BC}{MP}$