|
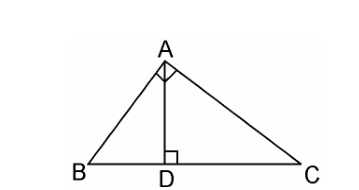
Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle
PQR. Show that Δ ABC ~ Δ PQR.
|
Answer
|
|
A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time
a tower casts a shadow 28 m long. Find the height of the tower.
|
Answer
|
|
If AD and PM are medians of triangles ABC and PQR, respectively where Δ ABC ~ Δ PQR, prove that $\dfrac{AB}{PQ} = \dfrac{AD}{PM}$
|
Answer
|
|
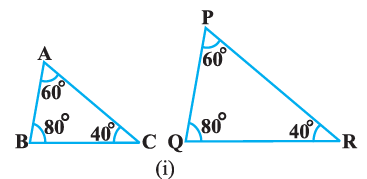
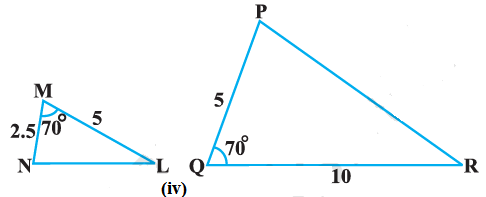
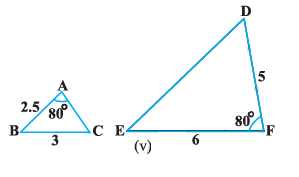
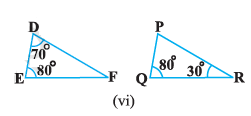
State which pairs of triangles in Fig are similar. Write the similarity criterion used by you for answering the question and also write the pairs
of similar triangles in the symbolic form :
|
Answer
|
|
In Fig 6.35, Δ ODC ~ Δ OBA, $\angle BOC = 125°$ and $\angle CDO = 70°$. Find $\angle DOC, \angle DCO$ and $\angle OAB$.

|
Answer
|
|
Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that $\dfrac{OA}{OC} = \dfrac{OB}{OD}$
|
Answer
|
|
In Fig. 6.36, $\dfrac{QR}{QS} = \dfrac{QT}{PR}$ and $ \angle 1 = \angle 2$. Show that Δ PQS ~ Δ TQR.

|
Answer
|
|
S and T are points on sides PR and QR of Δ PQR such that $\angle P = \angle RTS$. Show that Δ RPQ ~ Δ RTS.
|
Answer
|
|
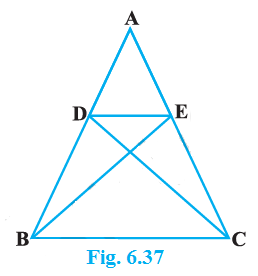
In Fig. 6.37, if Δ ABE ≅ Δ ACD, show that Δ ADE ~ Δ ABC.
|
Answer
|
|
In Fig. 6.38, altitudes AD and CE of Δ ABC intersect each other at the point P. Show that:
|
(i) Δ AEP ~ Δ CDP
(ii) Δ ABD ~ Δ CBE
(iii) Δ AEP ~ Δ ADB
(iv) Δ PDC ~ Δ BEC | 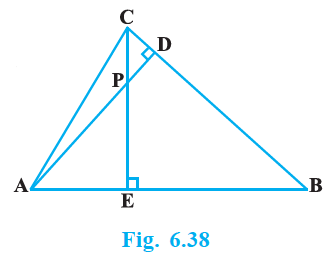
|
|
Answer
|