Tick the correct answer and justify : In Δ ABC, AB = 6 3 cm, AC = 12 cm and BC = 6 cm. The angle B is :
Given, in ΔABC, AB = 6 $\sqrt{3}$ cm, AC = 12 cm and BC = 6 cm.
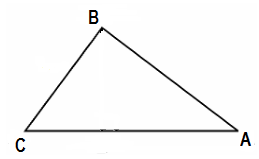
We can observe that,
$AB^2 $= 108
$AC^2$ = 144
And, $BC^2$= 36
$AB^2 + BC^2 = AC^2$
The given triangle, ΔABC, is satisfying Pythagoras theorem.
Therefore, the triangle is a right triangle, right-angled at B.
$\angle B = 90°$
Hence, the correct answer is (C).