In Fig. 6.54, O is a point in the interior of a triangle ABC, OD $\perp$ BC, OE $\perp$ AC and OF $\perp$ AB. Show that
(i) $OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2 = AF^2 + BD^2 + CE^2$
(ii) $AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2$
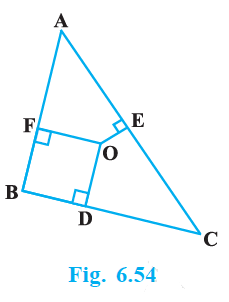
Given, in ΔABC, O is a point in the interior of a triangle
And OD $\perp$ BC, OE $\perp$ AC and OF $\perp$ AB
Join OA, OB and OC

(i) $OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2 = AF^2 + BD^2 + CE^2$
By Pythagoras theorem in ΔAOF, we have
$OA^2 = OF^2 + AF^2$
Similarly, in ΔBOD
$OB^2 = OD^2 + BD^2$
Similarly, in ΔCOE
$OC^2 = OE^2 + EC^2$
Adding these equations,
$OA^2 + OB^2 + OC^2 = OF^2 + AF^2 + OD^2 + BD^2 + OE^2 + EC^2$
$OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2 = AF^2 + BD^2 + CE^2$
(ii) $AF^2 + BD^2 + EC^2 = (OA^2 – OE^2) + (OC^2 – OD^2) + (OB^2 – OF^2)$
$ AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2$