Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the p

For Competitive Exams

Question 12 Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.

Solution:

Given, Two poles of heights 6 m and 11 m stand on a plane ground.

And distance between the feet of the poles is 12 m.

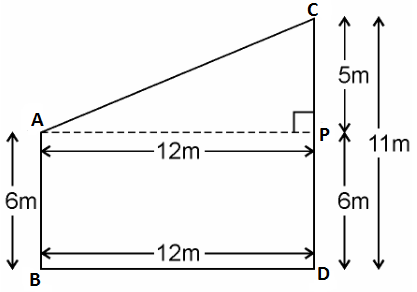
Let AB and CD be the poles of height 6m and 11m.

Therefore, CP = 11 – 6 = 5m

From the figure, it can be observed that AP = 12m

By Pythagoras theorem for ΔAPC, we get,

$AP^2 = PC^2 + AC^2$

$(12m)^2 + (5m)^2 = (AC)^2$

$AC^2 = (144+25) m^2 = 169 m^2$

AC = 13m

Therefore, the distance between their tops is 13 m.

Additional Questions

D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that $AE^2 + BD^2 = AB^2 + DE^2$.	Answer
The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3 CD (see Fig. 6.55). Prove that $2 AB^2 = 2 AC^2 + BC2$		Answer
In an equilateral triangle ABC, D is a point on side BC such that BD = $\dfrac{1}{3BC}$. Prove that $9 AD^2 = 7 AB^2$.	Answer
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.	Answer
Tick the correct answer and justify : In Δ ABC, AB = 6 3 cm, AC = 12 cm and BC = 6 cm. The angle B is :	Answer
Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse. (i) 7 cm, 24 cm, 25 cm (ii) 3 cm, 8 cm, 6 cm (iii) 50 cm, 80 cm, 100 cm (iv) 13 cm, 12 cm, 5 cm	Answer
PQR is a triangle right angled at P and M is a point on QR such that PM $\perp$ QR. Show that $PM^2$ = QM . MR.	Answer
In Fig. 6.53, ABD is a triangle right angled at A and AC $\perp$ BD. Show that (i) $AB^2$ = BC . BD (ii) $AC^2$ = BC . DC (iii) $AD^2$ = BD . CD		Answer
ABC is an isosceles triangle right angled at C. Prove that $AB^2 = 2AC^2$	Answer
ABC is an isosceles triangle with AC = BC. If $AB^2 = 2 AC^2$, prove that ABC is a right triangle.	Answer

Share with Friends