Question 16
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
Solution:
Given, an equilateral triangle say ABC
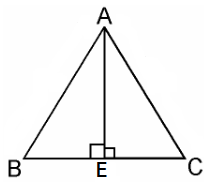
Let the sides of the equilateral triangle be of length a, and AE be the altitude of ΔABC
BE = EC = $\dfrac{BC}{2} = \dfrac{a}{2}$
In ΔABE, by Pythagoras Theorem, we get
$AB^2 = AE^2 + BE^2$
$a^{2}= AE^{2}+(\dfrac{a}{2})^2$
$AE^{2}=a^{2}-\dfrac{a^2}{4}$
$AE^{2}= \dfrac{3a^2}{4}$
$4AE^2 = 3a^2$
4 × (Square of altitude) = 3 × (Square of one side)
Hence, proved.
