PQR is a triangle right angled at P and M is a point on QR such that PM \perp QR. Show that PM^2

For Competitive Exams

Question 2 PQR is a triangle right angled at P and M is a point on QR such that PM $\perp$ QR. Show that $PM^2$ = QM . MR.

Solution:

Given, ΔPQR is right angled at P is a point on QR such that PM $\perp$ QR

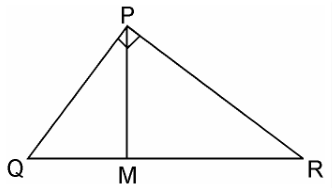
We have to prove, $PM^2$ = QM × MR

In ΔPQM, by Pythagoras theorem

$PQ^2 = PM^2 + QM^2$

Or, $PM^2 = PQ^2 – QM^2$ ……………………………..(i)

In ΔPMR, by Pythagoras theorem

$PR^2 = PM^2 + MR^2$

Or, $PM^2 = PR^2 – MR^2$ ………………………………………..(ii)

Adding equation, (i) and (ii), we get

$2PM^2 = (PQ^2 + PM^2) – (QM^2 + MR^2)$

= $QR^2 – QM^2 – MR^2 [∴ QR^2 = PQ^2 + PR^2]$

= $(QM + MR)^2 – QM^2 – MR^2$

= 2QM × MR

$PM^2$ = QM × MR

Additional Questions

In Fig. 6.53, ABD is a triangle right angled at A and AC $\perp$ BD. Show that (i) $AB^2$ = BC . BD (ii) $AC^2$ = BC . DC (iii) $AD^2$ = BD . CD		Answer
ABC is an isosceles triangle right angled at C. Prove that $AB^2 = 2AC^2$	Answer
ABC is an isosceles triangle with AC = BC. If $AB^2 = 2 AC^2$, prove that ABC is a right triangle.	Answer
ABC is an equilateral triangle of side 2a. Find each of its altitudes.	Answer
Prove that the sum of the squares of the sides of rhombus is equal to the sum of the squares of its diagonals.	Answer
In Fig. 6.54, O is a point in the interior of a triangle ABC, OD $\perp$ BC, OE $\perp$ AC and OF $\perp$ AB. Show that (i) $OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2 = AF^2 + BD^2 + CE^2$ (ii) $AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2$		Answer
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall.	Answer
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?	Answer
An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of1200 km per hour. How far apart will be the two planes after $1\dfrac{1}{2}$ hours?	Answer
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.	Answer

Share with Friends