|
An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of1200 km per hour. How far apart will be the two planes after $1\dfrac{1}{2}$ hours?
|
Answer
|
|
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.
|
Answer
|
|
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that $AE^2 + BD^2 = AB^2 + DE^2$.
|
Answer
|
|
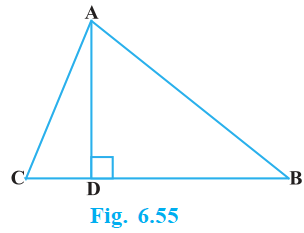
The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3 CD (see Fig. 6.55). Prove that $2 AB^2 = 2 AC^2 + BC2$
|  |
Answer
|
|
In an equilateral triangle ABC, D is a point on side BC such that BD = $\dfrac{1}{3BC}$. Prove that
$9 AD^2 = 7 AB^2$.
|
Answer
|
|
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.
|
Answer
|
|
Tick the correct answer and justify : In Δ ABC, AB = 6 3 cm, AC = 12 cm and BC = 6 cm.
The angle B is :
|
Answer
|
|
Sides of triangles are given below. Determine which of them are right triangles.
In case of a right triangle, write the length of its hypotenuse.
(i) 7 cm, 24 cm, 25 cm
(ii) 3 cm, 8 cm, 6 cm
(iii) 50 cm, 80 cm, 100 cm
(iv) 13 cm, 12 cm, 5 cm
|
Answer
|
|
PQR is a triangle right angled at P and M is a point on QR such that PM $\perp$ QR. Show that $PM^2$ = QM . MR.
|
Answer
|
|
In Fig. 6.53, ABD is a triangle right angled at A and AC $\perp$ BD. Show that
(i) $AB^2$ = BC . BD
(ii) $AC^2$ = BC . DC
(iii) $AD^2$ = BD . CD
|  |
Answer
|



