Question 14
The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3 CD (see Fig. 6.55). Prove that $2 AB^2 = 2 AC^2 + BC2$
Solution:
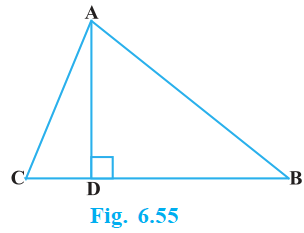
Given, the perpendicular from A on side BC of a Δ ABC intersects BC at D such that
DB = 3CD
In Δ ABC
AD $\perp$ BC and BD = 3CD
In right angle triangle, ADB and ADC, by Pythagoras theorem,
$AB^2 = AD^2 + BD^2$ ……………………….(i)
$AC^2 = AD^2 + DC^2 $……………………………..(ii)
Subtracting equation (ii) from equation (i), we get
$AB^2 – AC^2 = BD^2 – DC^2$
= $9CD^2 – CD^2$ [Since, BD = 3CD]
= $8CD^2$
= $8(\dfrac{BC}{4})^2$ [Since, BC = DB + CD = 3CD + CD = 4CD]
Therefore, $AB^2 – AC^2 = \dfrac{BC^2}{2}$
$2(AB^2 – AC^2) = BC^2$
$2AB^2 – 2AC^2 = BC^2$
$2AB^2 = 2AC^2 + BC^2$
