In an equilateral triangle ABC, D is a point on side BC such that BD = \dfrac{1}{3BC}. Prove that

For Competitive Exams

Question 15 In an equilateral triangle ABC, D is a point on side BC such that BD = $\dfrac{1}{3BC}$. Prove that $9 AD^2 = 7 AB^2$.

Solution:

Given, ABC is an equilateral triangle

And D is a point on side BC such that BD = $\dfrac{1}{3BC}$

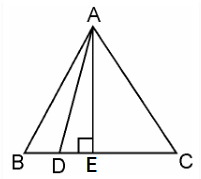
Let the side of the equilateral triangle be a, and AE be the altitude of ΔABC

BE = EC = $\dfrac{BC}{2} = \dfrac{a}{2}$

And, AE = $a\dfrac{\sqrt{3}}{2}$

Given, BD = $\dfrac{1}{3BC}$

BD =$\dfrac{a}{3}$

DE = BE – BD = $\dfrac{a}{2} – \dfrac{a}{3} = \dfrac{a}{6}$

In ΔADE, by Pythagoras theorem

$AD^2 = AE^2 + DE^2$

$AD^2 = (\dfrac{a\sqrt{3}}{2})^2 + (\dfrac{a}{6})^2$

$AD^2 = \dfrac{3a^2}{4} + \dfrac{a^2}{36}$

$AD^2 = \dfrac{28a^2}{36}$

$AD^2 = \dfrac{7}{9} AB^2$

$9 AD^2 = 7 AB^2$

Additional Questions

In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.	Answer
Tick the correct answer and justify : In Δ ABC, AB = 6 3 cm, AC = 12 cm and BC = 6 cm. The angle B is :	Answer
Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse. (i) 7 cm, 24 cm, 25 cm (ii) 3 cm, 8 cm, 6 cm (iii) 50 cm, 80 cm, 100 cm (iv) 13 cm, 12 cm, 5 cm	Answer
PQR is a triangle right angled at P and M is a point on QR such that PM $\perp$ QR. Show that $PM^2$ = QM . MR.	Answer
In Fig. 6.53, ABD is a triangle right angled at A and AC $\perp$ BD. Show that (i) $AB^2$ = BC . BD (ii) $AC^2$ = BC . DC (iii) $AD^2$ = BD . CD		Answer
ABC is an isosceles triangle right angled at C. Prove that $AB^2 = 2AC^2$	Answer
ABC is an isosceles triangle with AC = BC. If $AB^2 = 2 AC^2$, prove that ABC is a right triangle.	Answer
ABC is an equilateral triangle of side 2a. Find each of its altitudes.	Answer
Prove that the sum of the squares of the sides of rhombus is equal to the sum of the squares of its diagonals.	Answer
In Fig. 6.54, O is a point in the interior of a triangle ABC, OD $\perp$ BC, OE $\perp$ AC and OF $\perp$ AB. Show that (i) $OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2 = AF^2 + BD^2 + CE^2$ (ii) $AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2$		Answer

Share with Friends