Given, ABC is an equilateral triangle of side 2a
Draw, AD $\perp$ BC
In ΔADB and ΔADC
AB = AC
AD = AD
$\angle ADB = \angle ADC$ [Both are 90°]
Therefore, ΔADB ≅ ΔADC by RHS congruence
Hence, BD = DC [by CPCT]
In right angled ΔADB
$AB^2 = AD^2 + BD^2$
$(2a)^2 = AD^2 + a^2 $
$AD^2 = 4a^2 – a^2$
$AD^2 = 3a^2$
AD = $\sqrt{3a}$
|
Prove that the sum of the squares of the sides of rhombus is equal to the sum of the squares of its diagonals. |
Answer | |
|
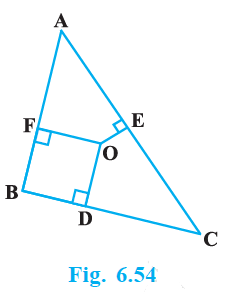
In Fig. 6.54, O is a point in the interior of a triangle ABC, OD $\perp$ BC, OE $\perp$ AC and OF $\perp$ AB. Show that (i) $OA^2 + OB^2 + OC^2 – OD^2 – OE^2 – OF^2 = AF^2 + BD^2 + CE^2$ (ii) $AF^2 + BD^2 + CE^2 = AE^2 + CD^2 + BF^2$ |  |
Answer |
|
A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from base of the wall. |
Answer | |
|
A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut? |
Answer | |
|
An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of1200 km per hour. How far apart will be the two planes after $1\dfrac{1}{2}$ hours? |
Answer | |
|
Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops. |
Answer | |
|
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that $AE^2 + BD^2 = AB^2 + DE^2$. |
Answer | |
|
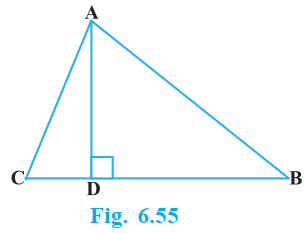
The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3 CD (see Fig. 6.55). Prove that $2 AB^2 = 2 AC^2 + BC2$ |  |
Answer |
|
In an equilateral triangle ABC, D is a point on side BC such that BD = $\dfrac{1}{3BC}$. Prove that $9 AD^2 = 7 AB^2$. |
Answer | |
|
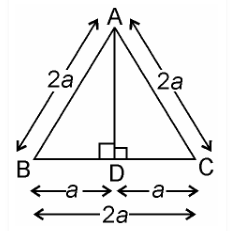
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes. |
Answer |