An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time,

For Competitive Exams

Question 11 An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of1200 km per hour. How far apart will be the two planes after $1\dfrac{1}{2}$ hours?

Solution:

Given

Speed of first aeroplane = 1000 km/hr

Distance covered by first aeroplane flying due north in

$1\dfrac{1}{2}$ hours (OA) = 1000 × $\dfrac{3}{2}$ km = 1500 km

Speed of second aeroplane = 1200 km/hr

Distance covered by second aeroplane flying due west in

$1\dfrac{1}{2}$ hours (OB) = 1200 × $\dfrac{3}{2}$ km = 1800 km

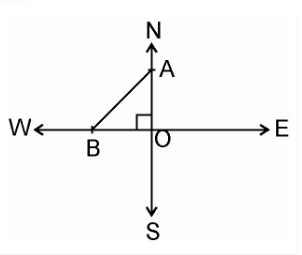
In right angle ΔAOB, by Pythagoras Theorem,

AB^2 = AO^2 + OB^2

AB2 = $(1500)^2 + (1800)^2$

AB = $\sqrt{(2250000 + 3240000)}$

= $\sqrt{5490000}$

AB = 300$\sqrt{61}$ km

Hence, the distance between two aeroplanes will be 300 $\sqrt{61}$ km.

Additional Questions

Two poles of heights 6 m and 11 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.	Answer
D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that $AE^2 + BD^2 = AB^2 + DE^2$.	Answer
The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3 CD (see Fig. 6.55). Prove that $2 AB^2 = 2 AC^2 + BC2$		Answer
In an equilateral triangle ABC, D is a point on side BC such that BD = $\dfrac{1}{3BC}$. Prove that $9 AD^2 = 7 AB^2$.	Answer
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.	Answer
Tick the correct answer and justify : In Δ ABC, AB = 6 3 cm, AC = 12 cm and BC = 6 cm. The angle B is :	Answer
Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse. (i) 7 cm, 24 cm, 25 cm (ii) 3 cm, 8 cm, 6 cm (iii) 50 cm, 80 cm, 100 cm (iv) 13 cm, 12 cm, 5 cm	Answer
PQR is a triangle right angled at P and M is a point on QR such that PM $\perp$ QR. Show that $PM^2$ = QM . MR.	Answer
In Fig. 6.53, ABD is a triangle right angled at A and AC $\perp$ BD. Show that (i) $AB^2$ = BC . BD (ii) $AC^2$ = BC . DC (iii) $AD^2$ = BD . CD		Answer
ABC is an isosceles triangle right angled at C. Prove that $AB^2 = 2AC^2$	Answer

Share with Friends