D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove th

For Competitive Exams

Question 13 D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C. Prove that $AE^2 + BD^2 = AB^2 + DE^2$.

Solution:

Given, D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C.

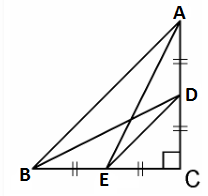
By Pythagoras theorem in ΔACE, we get

$AC^2 + CE^2 = AE^2$ ………………………………………….(i)

In ΔBCD, by Pythagoras theorem, we get

$BC^2 + CD^2 = BD^2$ ………………………………..(ii)

From equations (i) and (ii), we get,

$AC^2 + CE^2 + BC^2 + CD^2 = AE^2 + BD^2$ …………..(iii)

In ΔCDE, by Pythagoras theorem, we get

$DE^2 = CD^2 + CE^2$

In ΔABC, by Pythagoras theorem, we get

$AB^2 = AC^2 + CB^2$

Putting the above two values in equation (iii), we get

$DE^2 + AB^2 = AE^2 + BD^2$

Additional Questions

The perpendicular from A on side BC of a Δ ABC intersects BC at D such that DB = 3 CD (see Fig. 6.55). Prove that $2 AB^2 = 2 AC^2 + BC2$		Answer
In an equilateral triangle ABC, D is a point on side BC such that BD = $\dfrac{1}{3BC}$. Prove that $9 AD^2 = 7 AB^2$.	Answer
In an equilateral triangle, prove that three times the square of one side is equal to four times the square of one of its altitudes.	Answer
Tick the correct answer and justify : In Δ ABC, AB = 6 3 cm, AC = 12 cm and BC = 6 cm. The angle B is :	Answer
Sides of triangles are given below. Determine which of them are right triangles. In case of a right triangle, write the length of its hypotenuse. (i) 7 cm, 24 cm, 25 cm (ii) 3 cm, 8 cm, 6 cm (iii) 50 cm, 80 cm, 100 cm (iv) 13 cm, 12 cm, 5 cm	Answer
PQR is a triangle right angled at P and M is a point on QR such that PM $\perp$ QR. Show that $PM^2$ = QM . MR.	Answer
In Fig. 6.53, ABD is a triangle right angled at A and AC $\perp$ BD. Show that (i) $AB^2$ = BC . BD (ii) $AC^2$ = BC . DC (iii) $AD^2$ = BD . CD		Answer
ABC is an isosceles triangle right angled at C. Prove that $AB^2 = 2AC^2$	Answer
ABC is an isosceles triangle with AC = BC. If $AB^2 = 2 AC^2$, prove that ABC is a right triangle.	Answer
ABC is an equilateral triangle of side 2a. Find each of its altitudes.	Answer

Share with Friends