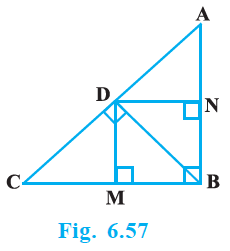
By applying Pythagoras Theorem in ∆ADB, we get,
$AB^2 = AD^2 + DB^2$ ……………………… (i)
Again, by applying Pythagoras Theorem in ∆ACD, we get,
$AC^2 = AD^2 + DC^2$
$AC^2 = AD^2 + (DB + BC)^2$
$AC^2 = AD^2 + DB^2 + BC^2 + 2DB × BC$
From equation (i), we can write,
$AC^2 = AB^2 + BC^2 + 2DB × BC$
Hence, proved.