Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squar

Question 6 Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.

Solution:

Let us consider, ABCD be a parallelogram. Now, draw perpendicular DE on extended side of AB, and draw a perpendicular AF meeting DC at point F.

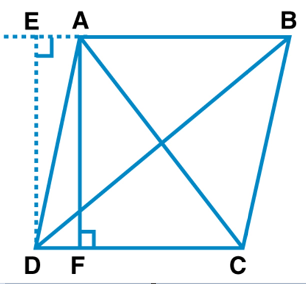
By applying Pythagoras Theorem in ∆DEA, we get,

$DE^2 + EA^2 = DA^2 $……………….… (i)

By applying Pythagoras Theorem in ∆DEB, we get,

$DE^2 + EB^2 = DB^2$

$DE^2 + (EA + AB)^2 = DB^2$

$(DE^2 + EA^2) + AB^2 + 2EA × AB = DB^2$

$DA^2 + AB^2 + 2EA × AB = DB^2$ ……………. (ii)

By applying Pythagoras Theorem in ∆ADF, we get,

$AD^2 = AF^2 + FD^2$

Again, applying Pythagoras theorem in ∆AFC, we get,

$AC^2 = AF^2 + FC^2 = AF^2 + (DC − FD)^2$

$= AF^2 + DC^2 + FD^2 − 2DC × FD$

$= (AF^2 + FD^2) + DC^2 − 2DC × FD AC^2$

$AC^2= AD^2 + DC^2 − 2DC × FD$ ………………… (iii)

Since ABCD is a parallelogram,

AB = CD ………………….…(iv)

And BC = AD ………………. (v)

In ∆DEA and ∆ADF,

$\angle DEA = \angle AFD$ (Each 90°)

$\angle EAD = \angle ADF (EA || DF)$

AD = AD (Common Angles)

∆EAD ≅ ∆FDA (AAS congruence criterion)

EA = DF ……………… (vi)

Adding equations (i) and (iii), we get,

$DA^2 + AB^2 + 2EA × AB + AD^2 + DC^2 − 2DC × FD = DB^2 + AC^2$

$DA^2 + AB^2 + AD^2 + DC^2 + 2EA × AB − 2DC × FD = DB^2 + AC^2$

From equation (iv) and (vi),

$BC^2 + AB^2 + AD^2 + DC^2 + 2EA × AB − 2AB × EA = DB^2 + AC^2$

$AB^2 + BC^2 + CD^2 + DA^2 = AC^2 + BD^2$

In Fig. 6.61, two chords AB and CD intersect each other at the point P. Prove that : (i) Δ APC ~ Δ DPB (ii) AP . PB = CP . DP		Answer
In Fig. 6.62, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that (i) Δ PAC ~ Δ PDB (ii) PA . PB = PC . PD		Answer
In Fig. 6.63, D is a point on side BC of Δ ABC such that $\dfrac{BD}{CD} = \dfrac{AB}{AC}$ Prove that AD is the bisector of $\angle BAC$.		Answer
Nazima is fly fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (see Fig. 6.64)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?		Answer
In Fig. 6.56, PS is the bisector of $\angle QPR$ of Δ PQR. Prove that $\dfrac{QS}{SR} = \dfrac{PQ}{PR}$		Answer
In Fig. 6.57, D is a point on hypotenuse AC of Δ ABC, such that BD $\perp$ AC, DM $\perp$ BC and DN $\perp$ AB. Prove that : (i) $DM^2 = DN . MC $ (ii) $DN^2 = DM . AN $		Answer
In Fig. 6.58, ABC is a triangle in which $\angle ABC > 90°$ and AD $\perp$ CB produced. Prove that $AC^2 = AB^2 + BC^2 + 2 BC . BD.$		Answer
In Fig. 6.59, ABC is a triangle in which $\angle ABC < 90°$ and AD $\perp$ BC. Prove that $AC^2 = AB^2 + BC^2 – 2 BC.BD.$		Answer
In Fig. 6.60, AD is a median of a triangle ABC and AM ⊥ BC. Prove that : (i)$ AC^2 = AD^2 + BC . DM + (\dfrac{BC}{2})^2$ (ii) $AB^2 = AD^2 – BC . DM + (\dfrac{BC}{2})^2$ (iii) $AC^2 + AB^2 = 2 AD^2 + \dfrac{1}{2} BC^2$		Answer
Prove that the sum of the squares of the diagonals of parallelogram is equal to the sum of the squares of its sides.	Answer