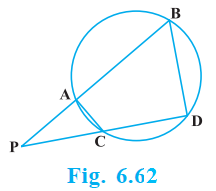
In Fig. 6.61, two chords AB and CD intersect each other at the point P. Prove that :
(i) Δ APC ~ Δ DPB
(ii) AP . PB = CP . DP

Firstly, let us join CB, in the given figure.
(i) In ∆APC and ∆DPB,
$\angle APC = \angle DPB$ (Vertically opposite angles)
$\angle CAP = \angle BDP$ (Angles in the same segment for chord CB)
Therefore,
∆APC ∼ ∆DPB (AA similarity criterion)
(ii) AP . PB = CP . DP
In the above, we have proved that ∆APC ∼ ∆DPB
We know that the corresponding sides of similar triangles are proportional.
$\dfrac{AP}{DP} = \dfrac{PC}{PB} = \dfrac{CA}{BD}$
$\dfrac{AP}{DP} = \dfrac{PC}{PB}$
∴AP. PB = PC. DP
Hence, proved.