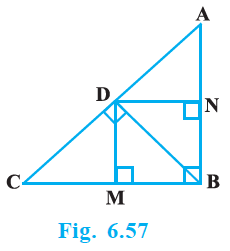
In Fig. 6.63, D is a point on side BC of Δ ABC such that $\dfrac{BD}{CD} = \dfrac{AB}{AC}$ Prove that AD is the bisector of $\angle BAC$.

In the given figure, let us extend BA to P such that;
AP = AC.
Now join PC
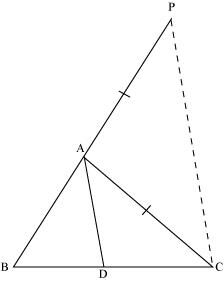
Given, $\dfrac{BD}{CD} = \dfrac{AB}{AC}$
$\dfrac{BD}{CD} = \dfrac{AP}{AC}$
By using the converse of basic proportionality theorem, we get,
AD || PC
$\angle BAD = \angle APC$ (Corresponding angles) ……………….. (i)
And, $\angle DAC = \angle ACP$ (Alternate interior angles) …….… (ii)
By the new figure, we have;
AP = AC
$\angle APC = \angle ACP$ ……………………. (iii)
On comparing equations (i), (ii), and (iii), we get,
$\angle BAD = \angle APC$
Therefore, AD is the bisector of the angle BAC.
Hence, proved.