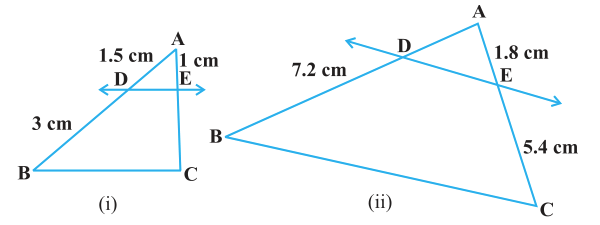
(i) Given, in △ ABC, DE∥BC
∴ $\dfrac{AD}{DB} = \dfrac{AE}{EC}$ [Using Basic proportionality theorem]
$\dfrac{1.5}{3} = \dfrac{1}{EC}$
EC = $\dfrac{3}{1.5}$
EC = $\dfrac{3 × 10}{15}$ = 2 cm
EC = 2cm
(ii) Given, in △ ABC, DE∥BC
∴ $\dfrac{AD}{DB} = \dfrac{AE}{EC}$ [Using Basic proportionality theorem]
$\dfrac{AD}{7.2} = \dfrac{1.8}{5.4}$
AD = $\dfrac{1.8 × 7.2}{5.4} = (\dfrac{18}{10})×(\dfrac{72}{10})×(\dfrac{10}{54}) = \dfrac{24}{10}$
AD = 2.4
Hence, AD = 2.4 cm.