Given, ABCD is a trapezium where AB || DC and diagonals AC and BD intersect each other at O.
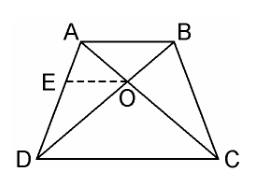
We have to prove, AO/BO = CO/DO
From the point O, draw a line EO touching AD at E, in such a way that,
EO || DC || AB
In ΔADC, we have OE || DC
Therefore, By using Basic Proportionality Theorem
$\dfrac{AE}{ED} = \dfrac{AO}{CO}$ ……………..(i)
Now, In ΔABD, OE || AB
Therefore, By using Basic Proportionality Theorem
$\dfrac{DE}{EA} = \dfrac{DO}{BO}$…………….(ii)
From equation (i) and (ii), we get,
$\dfrac{AO}{CO} = \dfrac{BO}{DO}$
$\dfrac{AO}{BO} = \dfrac{CO}{DO}$
Hence proved.