E and F are points on the sides PQ and PR respectively of a Δ PQR. For each of the followin

Question 2

E and F are points on the sides PQ and PR respectively of a Δ PQR.
For each of the following cases, state whether EF || QR :

(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm

(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm

(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm

Solution:

Given, in ΔPQR, E and F are two points on side PQ and PR, respectively. See the figure below

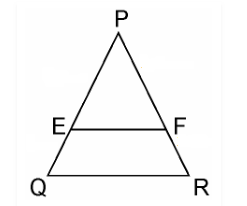
(i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm

by using Basic proportionality theorem

find $\dfrac{PE}{EQ}$ and $\dfrac{PF}{FR}$

$\dfrac{PE}{EQ} = \dfrac{3.9}{3} = \dfrac{39}{30} = \dfrac{13}{10} = 1.3$

$\dfrac{PF}{FR} = \dfrac{3.6}{2.4} = \dfrac{36}{24} = \dfrac{3}{2} = 1.5$

$\dfrac{PE}{EQ} \neq \dfrac{PF}{FR}$ , EF not Parallel QR

(ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm

by using Basic proportionality theorem

find $ \dfrac{PE}{EQ}$ and $\dfrac{PF}{FR}$

$\dfrac{PE}{QE} = \dfrac{4}{4.5} = \dfrac{40}{45} = \dfrac{8}{9}$

$\dfrac{ PF}{RF} = \dfrac{8}{9}$

$\dfrac{PE}{QE} = \dfrac{PF}{RF}$ , EF is Parallel to QR.

(iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm

by using Basic proportionality theorem

find $ \dfrac{PE}{EQ}$ and $\dfrac{PF}{FR}$

EQ = PQ – PE = 1.28 – 0.18 = 1.10 cm

FR = PR – PF = 2.56 – 0.36 = 2.20 cm

So, $\dfrac{PE}{EQ} = \dfrac{0.18}{1.10} = \dfrac{18}{110} = \dfrac{9}{55}$…………. (i)

$\dfrac{PE}{FR} = \dfrac{0.36}{2.20} = \dfrac{36}{220} = \dfrac{9}{55}$………… (ii)

$\dfrac{PE}{EQ} = \dfrac{PF}{FR},$ EF is parallel to QR.

In Fig. 6.18, if LM \|\| CB and LN \|\| CD, prove that $\dfrac{AM}{AB} = \dfrac{ AN}{AD}$	Answer
In Fig. 6.19, DE \|\| AC and DF \|\| AE. Prove that $\dfrac{BF}{FE} = {BE}{EC}$	Answer
In Fig. 6.20, DE \|\| OQ and DF \|\| OR. Show that EF \|\| QR.	Answer
In Fig. 6.21, A, B and C are points on OP, OQ and OR respectively such that AB \|\| PQ and AC \|\| PR. Show that BC \|\| QR.	Answer
Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).	Answer
Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).	Answer
ABCD is a trapezium in which AB \|\| DC and its diagonals intersect each other at the point O. Show that $\dfrac{AO}{BO} = \dfrac{CO}{DO}$	Answer
The diagonals of a quadrilateral ABCD intersect each other at the point O such that $\dfrac{AO}{BO} = \dfrac{CO}{DO}$ Show that ABCD is a trapezium.	Answer
In figure. (i) and (ii), DE \|\| BC. Find EC in (i) and AD in (ii).	Answer
E and F are points on the sides PQ and PR respectively of a Δ PQR. For each of the following cases, state whether EF \|\| QR : (i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm (ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm (iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm	Answer