The diagonals of a quadrilateral ABCD intersect each other at the point O such that \dfrac{AO}{BO}

For Competitive Exams

Question 10 The diagonals of a quadrilateral ABCD intersect each other at the point O such that $\dfrac{AO}{BO} = \dfrac{CO}{DO}$ Show that ABCD is a trapezium.

Solution:

Given,

Quadrilateral ABCD where AC and BD intersects each other at O such that, $\dfrac{AO}{BO} = \dfrac{CO}{DO}

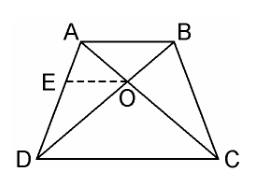
We have to prove here, ABCD is a trapezium

From the point O, draw a line EO touching AD at E, in such a way that,

EO || DC || AB

In ΔDAB, EO || AB

Therefore, By using Basic Proportionality Theorem

$\dfrac{DE}{EA} = \dfrac{DO}{OB}$……………………(i)

Also, given,

$\dfrac{AO}{BO} = \dfrac{CO}{DO}$

$\dfrac{AO}{CO} = \dfrac{BO}{DO}$

$\dfrac{CO}{AO} = \dfrac{DO}{BO}$

$\dfrac{DO}{OB} = \dfrac{CO}{AO}$ …………………………..(ii)

From equation (i) and (ii), we get

$\dfrac{DE}{EA} = \dfrac{CO}{AO}$

Therefore, By using converse of Basic Proportionality Theorem,

EO || DC also EO || AB

AB || DC.

Hence, quadrilateral ABCD is a trapezium with AB || CD.

Additional Questions

In figure. (i) and (ii), DE \|\| BC. Find EC in (i) and AD in (ii).	Answer
E and F are points on the sides PQ and PR respectively of a Δ PQR. For each of the following cases, state whether EF \|\| QR : (i) PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm (ii) PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm (iii) PQ = 1.28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm	Answer
In Fig. 6.18, if LM \|\| CB and LN \|\| CD, prove that $\dfrac{AM}{AB} = \dfrac{ AN}{AD}$	Answer
In Fig. 6.19, DE \|\| AC and DF \|\| AE. Prove that $\dfrac{BF}{FE} = {BE}{EC}$	Answer
In Fig. 6.20, DE \|\| OQ and DF \|\| OR. Show that EF \|\| QR.	Answer
In Fig. 6.21, A, B and C are points on OP, OQ and OR respectively such that AB \|\| PQ and AC \|\| PR. Show that BC \|\| QR.	Answer
Using Theorem 6.1, prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side. (Recall that you have proved it in Class IX).	Answer
Using Theorem 6.2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side. (Recall that you have done it in Class IX).	Answer
ABCD is a trapezium in which AB \|\| DC and its diagonals intersect each other at the point O. Show that $\dfrac{AO}{BO} = \dfrac{CO}{DO}$	Answer
The diagonals of a quadrilateral ABCD intersect each other at the point O such that $\dfrac{AO}{BO} = \dfrac{CO}{DO}$ Show that ABCD is a trapezium.	Answer

Share with Friends