Given, in ΔABC, D and E are the mid points of AB and AC respectively, such that, AD=BD and AE=EC.
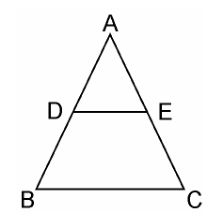
We have to prove that: DE || BC.
Since, D is the midpoint of AB
∴ AD = DB
$\dfrac{AD}{BD}$ = 1……………………………….. (i)
Also given, E is the mid-point of AC.
∴ AE = EC
$\dfrac{AE}{EC}$ = 1……………………………….. (ii)
From equation (i) and (ii), we get,
$\dfrac{AD}{BD} = \dfrac{AE}{EC}$
By converse of Basic Proportionality Theorem,
DE || BC
Hence, proved.