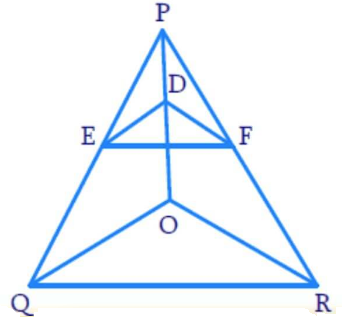
Given,
In ΔOPQ, AB || PQ
By using Basic Proportionality Theorem,
$\dfrac{OA}{AP} = \dfrac{OB}{BQ}$…………….(i)
Also given,
In ΔOPR, AC || PR
By using Basic Proportionality Theorem
∴ $\dfrac{OA}{AP} = \dfrac{OC}{CR}$……………(ii)
From equation (i) and (ii), we get,
$\dfrac{OB}{BQ} = \dfrac{OC}{CR}$
Therefore, by converse of Basic Proportionality Theorem,
In ΔOQR, BC || QR.