Given

Speed of first aeroplane = 1000 km/hr

Distance covered by first aeroplane flying due north in

$1\dfrac{1}{2}$ hours (OA) = 1000 × $\dfrac{3}{2}$ km = 1500 km

Speed of second aeroplane = 1200 km/hr

Distance covered by second aeroplane flying due west in

$1\dfrac{1}{2}$ hours (OB) = 1200 × $\dfrac{3}{2}$ km = 1800 km

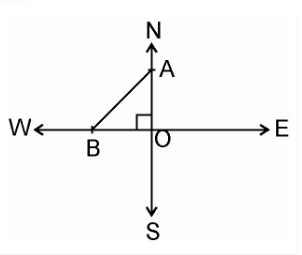
In right angle ΔAOB, by Pythagoras Theorem,

AB^2 = AO^2 + OB^2

AB2 = $(1500)^2 + (1800)^2$

AB = $\sqrt{(2250000 + 3240000)}$

= $\sqrt{5490000}$

AB = 300$\sqrt{61}$ km

Hence, the distance between two aeroplanes will be 300 $\sqrt{61}$ km.

Given, Two poles of heights 6 m and 11 m stand on a plane ground.

And distance between the feet of the poles is 12 m.

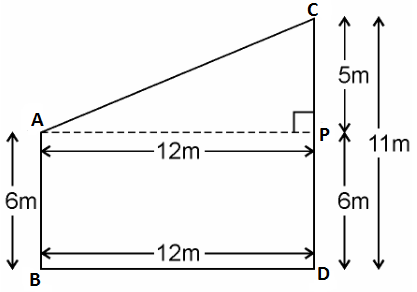
Let AB and CD be the poles of height 6m and 11m.

Therefore, CP = 11 – 6 = 5m

From the figure, it can be observed that AP = 12m

By Pythagoras theorem for ΔAPC, we get,

$AP^2 = PC^2 + AC^2$

$(12m)^2 + (5m)^2 = (AC)^2$

$AC^2 = (144+25) m^2 = 169 m^2$

AC = 13m

Therefore, the distance between their tops is 13 m.

Given, D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C.

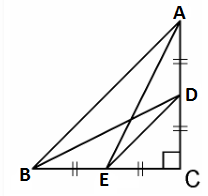
By Pythagoras theorem in ΔACE, we get

$AC^2 + CE^2 = AE^2$ ………………………………………….(i)

In ΔBCD, by Pythagoras theorem, we get

$BC^2 + CD^2 = BD^2$ ………………………………..(ii)

From equations (i) and (ii), we get,

$AC^2 + CE^2 + BC^2 + CD^2 = AE^2 + BD^2$ …………..(iii)

In ΔCDE, by Pythagoras theorem, we get

$DE^2 = CD^2 + CE^2$

In ΔABC, by Pythagoras theorem, we get

$AB^2 = AC^2 + CB^2$

Putting the above two values in equation (iii), we get

$DE^2 + AB^2 = AE^2 + BD^2$

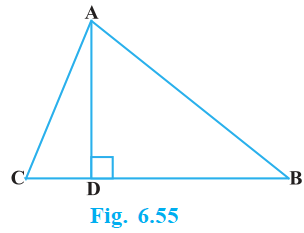
Given, the perpendicular from A on side BC of a Δ ABC intersects BC at D such that

DB = 3CD

In Δ ABC

AD $\perp$ BC and BD = 3CD

In right angle triangle, ADB and ADC, by Pythagoras theorem,

$AB^2 = AD^2 + BD^2$ ……………………….(i)

$AC^2 = AD^2 + DC^2 $……………………………..(ii)

Subtracting equation (ii) from equation (i), we get

$AB^2 – AC^2 = BD^2 – DC^2$

= $9CD^2 – CD^2$ [Since, BD = 3CD]

= $8CD^2$

= $8(\dfrac{BC}{4})^2$ [Since, BC = DB + CD = 3CD + CD = 4CD]

Therefore, $AB^2 – AC^2 = \dfrac{BC^2}{2}$

$2(AB^2 – AC^2) = BC^2$

$2AB^2 – 2AC^2 = BC^2$

$2AB^2 = 2AC^2 + BC^2$

Given, ABC is an equilateral triangle

And D is a point on side BC such that BD = $\dfrac{1}{3BC}$

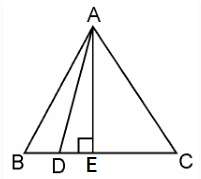
Let the side of the equilateral triangle be a, and AE be the altitude of ΔABC

BE = EC = $\dfrac{BC}{2} = \dfrac{a}{2}$

And, AE = $a\dfrac{\sqrt{3}}{2}$

Given, BD = $\dfrac{1}{3BC}$

BD =$\dfrac{a}{3}$

DE = BE – BD = $\dfrac{a}{2} – \dfrac{a}{3} = \dfrac{a}{6}$

In ΔADE, by Pythagoras theorem

$AD^2 = AE^2 + DE^2$

$AD^2 = (\dfrac{a\sqrt{3}}{2})^2 + (\dfrac{a}{6})^2$

$AD^2 = \dfrac{3a^2}{4} + \dfrac{a^2}{36}$

$AD^2 = \dfrac{28a^2}{36}$

$AD^2 = \dfrac{7}{9} AB^2$

$9 AD^2 = 7 AB^2$

Given, an equilateral triangle say ABC

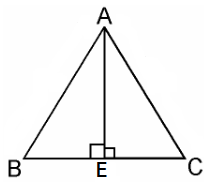
Let the sides of the equilateral triangle be of length a, and AE be the altitude of ΔABC

BE = EC = $\dfrac{BC}{2} = \dfrac{a}{2}$

In ΔABE, by Pythagoras Theorem, we get

$AB^2 = AE^2 + BE^2$

$a^{2}= AE^{2}+(\dfrac{a}{2})^2$

$AE^{2}=a^{2}-\dfrac{a^2}{4}$

$AE^{2}= \dfrac{3a^2}{4}$

$4AE^2 = 3a^2$

4 × (Square of altitude) = 3 × (Square of one side)

Hence, proved.